K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 12 2021
a: Xét tứ giác MNCP có
MP//CN
MN//CP
Do đó: MNCP là hình bình hành
7 tháng 1 2023
a: Xét tứ giác AIMK có
AI//MK
AK//MI
Do đó; AIMK là hình bình hành
b: để AIMK là hình chữ nhật thì góc A=90 độ
CM
25 tháng 2 2017
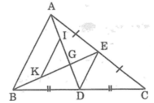
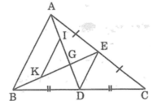
Vì AD và BE là 2 đường trung tuyến của ΔABC cắt nhau tại G nên theo tính chất đường trung tuyến, ta có: AG = 2/3 AD
CM
12 tháng 8 2017
Áp dụng kết quả bài 64 chương II sách Bài tập toán 7 vào ΔABC và ΔAGB ta có:
DE // AB và DE = 1/2 AB (1)
IK // AB và IK = 1/2 AB (2)
Từ (1) và (2) suy ra:
DE // IK và DE = IK.
8 tháng 4 2022
Bài 2:
a: Xét tứ giác AMCK có
I là trung điểm của AC
I là trug điểm của MK
Do đó: AMCK là hình bình hành
mà \(\widehat{AMC}=90^0\)
nên AMCK là hình chữ nhật
b: Để AMCK là hình vuông thì AM=CM
=>AM=BC/2
=>ΔABC vuông tại A
a: Xét ΔNAM và ΔNCP có
NA=NC
\(\widehat{ANM}=\widehat{CNP}\)(hai góc đối đỉnh)
NM=NP
Do đó: ΔNAM=ΔNCP
=>\(\widehat{NAM}=\widehat{NCP}\)
=>CP//AM
=>CP//AB
b: Xét ΔNAP và ΔNCM có
NA=NC
\(\widehat{ANP}=\widehat{CNM}\)(hai góc đối đỉnh)
NP=NM
Do đó: ΔNAP=ΔNCM
=>\(\widehat{NAP}=\widehat{NCM}\)
=>AP//CM
c: Xét ΔABC có
M,N lần lượt là trung điểm của AB,AC
=>MN là đường trung bình của ΔABC
=>MN//BC và \(MN=\dfrac{BC}{2}\)
Ta có: BC=2MN
mà MP=2MN
nên BC=MP
Ta có: ΔNAM=ΔNCP
=>AM=CP
=>CP=BM
Xét ΔMBC và ΔCPM có
MB=CP
BC=PM
MC chung
Do đó: ΔMBC=ΔCPM