Rút gọn các phân thức sau
\(\dfrac{x^2-4\sqrt{3}x+12}{x-2\sqrt{3}}\) với \(x\ne2\sqrt{3}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
19 tháng 4 2017
Qui tắc rút gọn một phân thức đại số.
- Phân tích tử và mẫu thành nhân tử (nếu cần) để tìm nhân tử chung.
- Chia cả tử và mẫu cho nhân tử chung đó.
Rút gọn:
CM
6 tháng 7 2018
a) Thay phân thức P vào biểu thức A rồi rút gọn chúng ta thu được A = u + v với điều kiện các biểu thức có nghĩa.
b) Tương tự a) ta có B = 1.
2 tháng 12 2021
\(\dfrac{10x^5y^2-30x^2y^6}{20x^2y^2}=\dfrac{10x^2y^2\left(x^3-3y^3\right)}{20x^2y^2}=\dfrac{x^3-3y^3}{2}\)
KV
2 tháng 12 2021
\(\dfrac{10x^5y^2-30x^2y^6}{20x^2y^2}=\dfrac{10x^2y^2\left(x^3-3y^4\right)}{10x^2y^2.2}=\dfrac{x^3-3y^4}{2}\)
1 tháng 12 2021
\(c,=\dfrac{x\left(x-y\right)}{5y\left(y-x\right)}=\dfrac{-x}{5y}\\ d,=\dfrac{x\left(x-y\right)-\left(x-y\right)}{x\left(x+y\right)-\left(x+y\right)}=\dfrac{\left(x-1\right)\left(x-y\right)}{\left(x-1\right)\left(x+y\right)}=\dfrac{x-y}{x+y}\)
NT
Nguyễn Thị Thùy Trang
Giáo viên
3 tháng 1 2022
\(\dfrac{x^2+x-2}{x^2+7x+10}=\dfrac{\left(x-1\right)\left(x+2\right)}{\left(x+2\right)\left(x+5\right)}=\dfrac{x-1}{x+5}\)
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 1 2022
\(=\dfrac{\left(x-1\right)\left(x+2\right)}{\left(x+2\right)\left(x+5\right)}=\dfrac{x-1}{x+5}\)
8 tháng 11 2021
\(=\dfrac{-3x\left(x-y\right)}{6y\left(y-x\right)}=\dfrac{-3x\left(x-y\right)}{-6y\left(x-y\right)}=\dfrac{x}{2y}\)
CM
16 tháng 9 2019
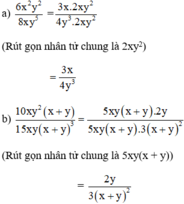
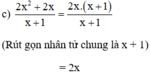
Phân tích tử số thành nhân tử :
x2 – xy – x + y = (x2 – xy) – (x – y) = x.(x – y) – (x – y) = (x – 1)(x – y)
+ Phân tích mẫu số thành nhân tử :
x2 + xy – x – y = (x2 + xy) – (x + y) = x(x + y) – (x + y) = (x – 1)(x + y)
Do đó ta có :
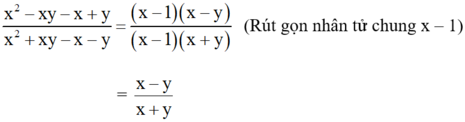
`(x^2 - 4sqrt{3}x + 12)/(x - 2sqrt{3}) (x ne 2sqrt{3})`
`= (x^2 - 2x . 2sqrt{3} + (2sqrt{3})^2)/(x - 2sqrt{3}) `
`= ( (x -2 sqrt{3} )^2)/(x - 2sqrt{3}) `
`= x - 2sqrt{3}`