so sánh 230 + 330 + 430và 3.2410
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giải toán trên mạng - Giúp tôi giải toán - Hỏi đáp, thảo luận về toán học - Học trực tuyến OLM
a: \(25S=25+5^4+...+5^{202}\)
=>24S=5^202-1
hay \(S=\dfrac{5^{202}-1}{24}\)
b:
4^30=2^30*2^30
=(2^3)^10*(2^2)^15>8^10*3^15=(8^10*3^10)*3^5>24^10*3
=>2^30+3^30+4^30>3*24^10

a,Tính tổng:S=1+52+54+...+5200
=>52S=52+54+56+...+5202
=>25S-S=24S=5202-1
=>S=\(\frac{5^{202}-1}{24}\)
b,So sánh 230+330+430 và 3.2410
3.24^10=3^11.4^15
4^30=4^15.4^15
hiển nhiên 4^15>3^11
=>3.24^10<<4^30<<<2^30+3^20+4^30
Ta có: 230+330+430>230+230+430=231+230.230
=231(1+229) (1)
Lại có:3.24^10=3^11.2^30 (2)
So sánh (1)và (2): Vì 3^11<4^11=2^22<2^29
và 2^30<2^31
=> 3^11.2^30 <(1+2^29)2^31<2^30+3^30+4^30

\(1,\\ \left(x-7\right)^{x+1}-\left(x-7\right)^{x+11}=0\\ \Leftrightarrow\left(x-7\right)^{x+1}\left[1-\left(x-7\right)^{10}\right]=0\\ \Leftrightarrow\left[{}\begin{matrix}\left(x-7\right)^{x+1}=0\\\left(x-7\right)^{10}=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x-7=0\\x-7=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=7\\x=8\end{matrix}\right.\)
\(2,\\ a,\left|2x-3\right|>5\Leftrightarrow\left[{}\begin{matrix}2x-3< -5\\2x-3>5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x< -1\\x>4\end{matrix}\right.\\ b,\left|3x-1\right|\le7\Leftrightarrow\left[{}\begin{matrix}3x-1\le7\\1-3x\le7\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x\le\dfrac{8}{3}\\x\ge-2\end{matrix}\right.\\ c,\cdot x< -\dfrac{3}{2}\\ \Leftrightarrow5-3x+\left(-2x-3\right)=7\Leftrightarrow2-5x=7\Leftrightarrow x=-1\left(ktm\right)\\ \cdot-\dfrac{3}{2}\le x\le\dfrac{5}{3}\\ \Leftrightarrow\left(5-3x\right)+\left(2x+3\right)=7\Leftrightarrow8-x=7\Leftrightarrow x=1\left(tm\right)\\ \cdot x>\dfrac{5}{3}\\ \Leftrightarrow\left(3x-5\right)+\left(2x+3\right)=7\Leftrightarrow5x-2=7\Leftrightarrow x=\dfrac{9}{5}\left(tm\right)\\ \Leftrightarrow S=\left\{1;\dfrac{9}{5}\right\}\)

a) \(3\cdot24^{10}=3\cdot6^{10}\cdot4^{10}=3\cdot3^{10}\cdot2^{10}\cdot2^{20}\)
\(=3^{11}\cdot2^{30}\)
\(4^{30}=2^{30}\cdot2^{30}=2^{30}\cdot4^{15}\)
Ta có \(4^{15}>3^{15}>3^{11}\) nên \(4^{15}>3^{11}\)
Khi đó \(4^{15}\cdot2^{30}>3^{11}\cdot2^{30}\) hay \(4^{30}>3\cdot24^{10}\)
b) \(\dfrac{3}{1^2\cdot2^2}+\dfrac{5}{2^2\cdot3^2}+...+\dfrac{19}{9^2\cdot10^2}\)
\(=\dfrac{3}{1\cdot4}+\dfrac{5}{4\cdot9}+...+\dfrac{19}{81\cdot100}\)
\(=1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{9}+...+\dfrac{1}{81}-\dfrac{1}{100}\)
\(=1-\dfrac{1}{100}=\dfrac{99}{100}< 1\)
Vậy dãy trên nhỏ hơn 1
a/
\(4^{30}=\left(2^2\right)^{30}=2^{60}=2^{30}.2^{30}=\left(2^2\right)^{15}.2^{30}=4^{15}.2^{30}\)
\(3.24^{10}=3.3^{10}.\left(2^3\right)^{10}=3^{11}.2^{30}< 3^{15}.2^{30}\)
\(\Rightarrow4^{30}=4^{15}.2^{30}>3^{15}.2^{30}>3^{11}.2^{30}=3.24^{10}\)
b/
\(=\dfrac{2^2-1^2}{1^2.2^2}+\dfrac{3^2-2^2}{2^2.3^2}+\dfrac{4^2-3^2}{3^2.4^2}+...+\dfrac{10^2-9^2}{9^2.10^2}=\)
\(=1-\dfrac{1}{2^2}+\dfrac{1}{2^2}-\dfrac{1}{3^2}+\dfrac{1}{3^2}-\dfrac{1}{4^2}+...+\dfrac{1}{9^2}-\dfrac{1}{10^2}=\)
\(=1-\dfrac{1}{10^2}< 1\)

Hãy so sánh 430 và 3.2410
Giải:
Ta có:
430 = 230 ∙ 230 = 230 ∙ (22)15 = 230 ∙ 415 = 230 ∙ 411 ∙ 44
3 ∙ 2410 = 3 ∙ (3.23)10 = 3 ∙ 310 ∙ 230 = 311 ∙ 230
Mà 411 ∙ 44 > 311 nên 430 > 3 ∙ 2410 .
\(4^{30}=\left(4^3\right)^{10}=64^{10}=\left(\dfrac{8}{3}\right)^{10}.24^{10}\\ Vì:\left(\dfrac{8}{3}\right)^{10}>3\Rightarrow\left(\dfrac{8}{3}\right)^{10}.24^{10}>3.24^{10}\\ \Rightarrow4^{30}>3.24^{10}\)


2515 = (52)15 = 530
810.330 = (23)10.330 = 230.330 = 630
Vì 530 < 630 (0<5<6)
=> 2515 < 810.330
\(25^{15}=\left(5^2\right)^{15}=5^{30}\)
\(8^{10}\cdot3^{30}=\left(2^3\right)^{10}\cdot3^{30}=2^{30}\cdot3^{30}=\left(2\cdot3\right)^{30}=6^{30}\)
Vì \(5< 6\) nên \(5^{30}< 6^{30}\)
Vậy \(25^{15}< 8^{10}\cdot3^{30}\)

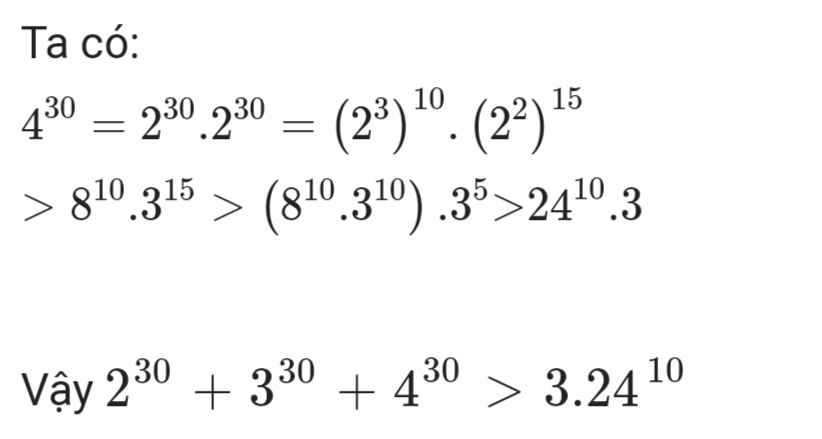
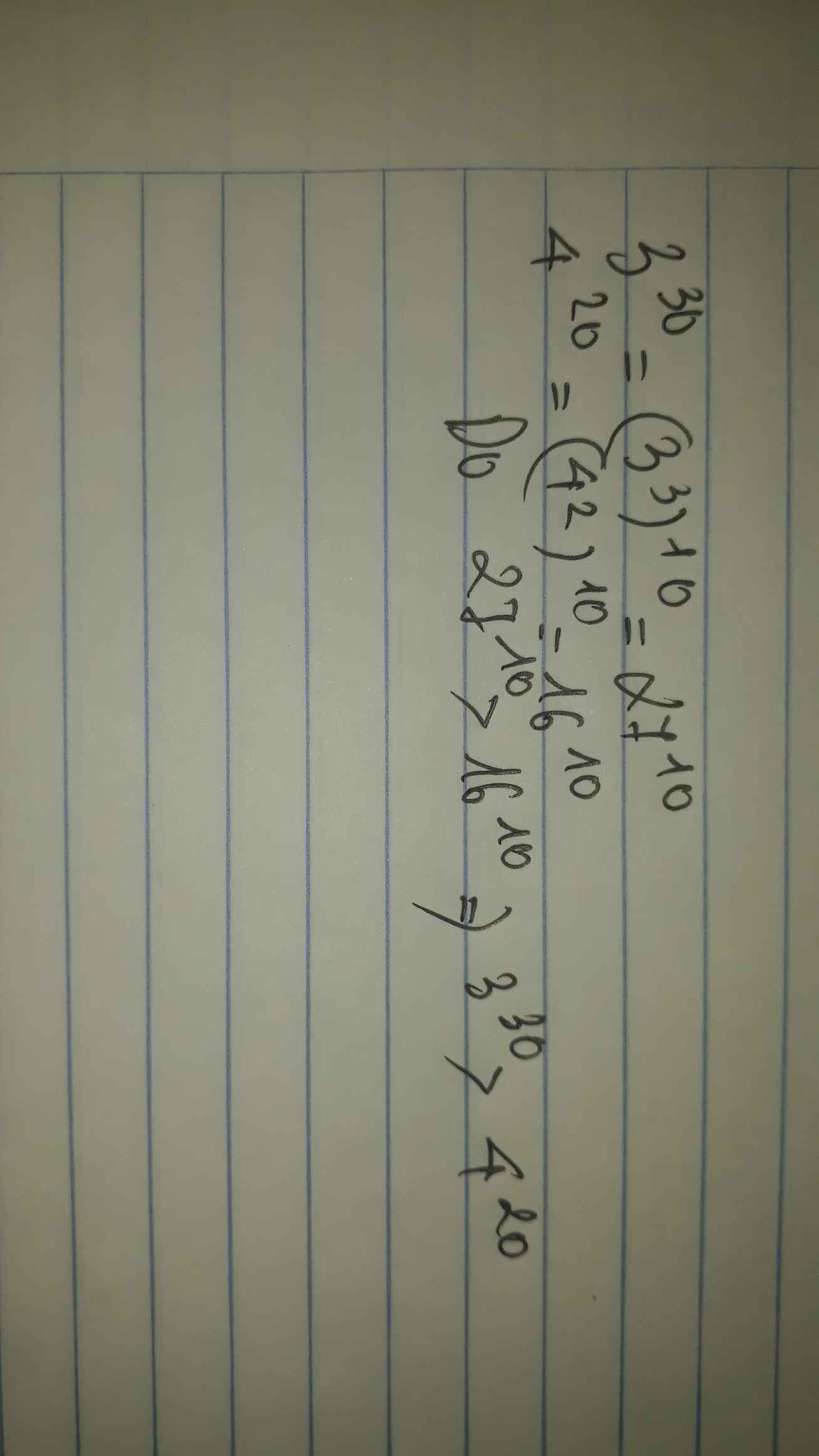
Ta có biến đổi:
\(4^{30}=2^{30}\cdot2^{30}\)
\(=\left(2^3\right)^{10}\cdot\left(2^2\right)^{15}>8^{10}\cdot3^{15}>\left(8^{10}\cdot3^{10}\right)\cdot3\)
\(=24^{10}\cdot3\)
Vậy\(2^{30}+3^{30}+4^{30}>3\cdot2^{24}\)