bài 2
Cho hình lăng trục đứng ABC.DEF có đáy là tam giác ABC vuông tại A. Biết AB = 3cm, AC = 4cm, CF =7cm
Tính diện tích toàn phần, diện tích xung quanh và thể tích hình lăng trụ trên.
giúp mik vs ạ. mik sẽ kb ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 12 2023
Chu vi đáy là 3+4+5=12(cm)
Diện tích xung quanh của hình trụ là:
\(S_{xq}=12\cdot7=84\left(cm^2\right)\)
Vì \(AB^2+AC^2=BC^2\)
nên ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot3\cdot4=6\left(cm^2\right)\)
Thể tích của lăng trụ là:
\(V=S_{đáy}\cdot cao=6\cdot7=42\left(cm^3\right)\)
9 tháng 5 2021
Áp dụng định lí Pitago vào △ABC:
⇒ BC2=√(AB2+AC2)=√(32+42)=5 cm
⇒ PABC=5+4+3=12 cm
Nên diện tích xung quanh của hình lăng trụ đứng ABC.DEF là:
Sxq=2p.h=12.6=72 cm2
Diện tích 2 đáy của hình lăng trụ đứng ABC.DEF là:
2.\(\dfrac{1}{2}\).3.4=12 cm2
Diện tích toàn phần của hình lăng trụ đứng ABC.DEF là:
72+12=84 cm2
Diện tích đáy của hình lăng trụ đứng ABC.DEF là:
\(\dfrac{1}{2}.3.4\)=6 cm2
Thể tích của hình lăng trụ đứng ABC.DEF là:
6.6=36 cm3
CM
4 tháng 8 2017
Đáp án C
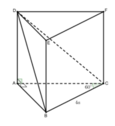
∆ A B C vuông
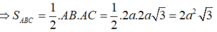
Đặt x =AD (x> 0)
∆ A B D vuông tại A
∆ A C D vuông tại A
Theo giả thiết, chu vi ∆ B C D bằng ( 9 + 17 ) a ta có phương trình:
Giải phương trình trên, ta tìm được
\(BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5\left(cm\right)\)
\(=>S_{xq}=\left(AB+AC+BC\right)\cdot CF=\left(3+4+5\right)\cdot7=84\left(cm^2\right)\)
Diện tích hai mặt đáy là: \(2S_đ=2\cdot\dfrac{1}{2}\cdot AB\cdot AC=2\cdot\dfrac{1}{2}\cdot3\cdot4=12\left(cm^2\right)\)
Diện tích toàn phần: \(S_{tp}=2S_đ+S_{xq}=84+12=96\left(cm^2\right)\)
Thể tích của hình lăng trụ là:
\(V=CF\cdot S_đ=7\cdot\dfrac{12}{2}=42\left(cm^3\right)\)
ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
Chu vi đáy là 3+4+5=12(cm)
Diện tích xung quanh là:
\(S_{xq}=12\cdot7=84\left(cm^2\right)\)
Diện tích đáy là: \(S_{đáy}=\dfrac{1}{2}\cdot3\cdot4=6\left(cm^2\right)\)
Diện tích toàn phần là: \(S_{tp}=S_{xq}+2\cdot S_{đáy}=84+2\cdot6=96\left(cm^2\right)\)
Thể tích là: \(V=S_{đáy}\cdot7=6\cdot7=42\left(cm^3\right)\)