\(\left(2x+3\right)^2\) \(=\) \(\dfrac{9}{121}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 2 2022
\(a,\left(x-6\right)\left(2x-5\right)\left(3x+9\right)=0\Leftrightarrow\left[{}\begin{matrix}x-6=0\Leftrightarrow x=6\\2x-5=0\Leftrightarrow x=\dfrac{5}{2}\\3x+9=0\Leftrightarrow x=-3\end{matrix}\right.\)
\(b,2x\left(x-3\right)+5\left(x-3\right)=0\Leftrightarrow\left(2x+5\right)\left(x-3\right)=0\Leftrightarrow\left[{}\begin{matrix}x-3=0\Leftrightarrow x=3\\2x+5=0\Leftrightarrow x=-\dfrac{5}{2}\end{matrix}\right.\)
\(c,x^2-4-\left(x-2\right)\left(3-2x\right)=0\Leftrightarrow\left(x-2\right)\left(x+2\right)-\left(x-2\right)\left(3-2x\right)=0\Leftrightarrow\left(x-2\right)\left(x+2-3+2x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{1}{3}\end{matrix}\right.\)
\(x=-7\left(2m-5\right)x-2m^2+8\Leftrightarrow x+7\left(2m-5\right)=8-2m^2\Leftrightarrow x\left(14m-34\right)=8-2m^2\)
\(ycđb\Leftrightarrow14m-34\ne0\Leftrightarrow m\ne\dfrac{34}{14}\)\(\Rightarrow x=\dfrac{8-2m^2}{14m-34}\)
\(3.17\Leftrightarrow4x^2-4x+1-2x-1=0\Leftrightarrow4x^2-6x=0\Leftrightarrow x\left(4x-6\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{3}{2}\end{matrix}\right.\)
DT
16 tháng 2 2022
3.15:
a, \(\Leftrightarrow\left\{{}\begin{matrix}x-6=0\\2x-5=0\\3x+9=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\x=\dfrac{5}{2}\\x=-\dfrac{9}{3}=-3\end{matrix}\right.\)
b, \(\Leftrightarrow\left(x-3\right)\left(2x+5\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-3=0\\2x+5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\x=-\dfrac{5}{2}\end{matrix}\right.\)
c, \(\Leftrightarrow\left(x-2\right)\left(x+2\right)-\left(x-2\right)\left(3-2x\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+2-3+2x\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2=0\\3x-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\x=\dfrac{1}{3}\end{matrix}\right.\)
3.16
\(\Leftrightarrow\left(2m-5\right).-7-2m^2+8=0\)
\(\Leftrightarrow-14m+35-2m^2+8=0\)
\(\Leftrightarrow-14m-2m^2+43=0\)
\(\Leftrightarrow-2\left(7m+m^2\right)=-43\)
\(\Leftrightarrow m\left(7-m\right)=\dfrac{43}{2}\)
\(\Leftrightarrow\dfrac{m\left(7-m\right)}{1}-\dfrac{43}{2}=0\)
\(\Leftrightarrow\dfrac{14m-2m^2}{2}-\dfrac{43}{2}=0\)
pt vô nghiệm
HP
7 tháng 8 2021
a, ĐK: \(x\le-1,x\ge3\)
\(pt\Leftrightarrow2\left(x^2-2x-3\right)+\sqrt{x^2-2x-3}-3=0\)
\(\Leftrightarrow\left(2\sqrt{x^2-2x-3}+3\right).\left(\sqrt{x^2-2x-3}-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x^2-2x-3}=-\dfrac{3}{2}\left(l\right)\\\sqrt{x^2-2x-3}=1\end{matrix}\right.\)
\(\Leftrightarrow x^2-2x-3=1\)
\(\Leftrightarrow x^2-2x-4=0\)
\(\Leftrightarrow x=1\pm\sqrt{5}\left(tm\right)\)
HP
7 tháng 8 2021
b, ĐK: \(-2\le x\le2\)
Đặt \(\sqrt{2+x}-2\sqrt{2-x}=t\Rightarrow t^2=10-3x-4\sqrt{4-x^2}\)
Khi đó phương trình tương đương:
\(3t-t^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=0\\t=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{2+x}-2\sqrt{2-x}=0\\\sqrt{2+x}-2\sqrt{2-x}=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2+x=8-4x\\2+x=17-4x+12\sqrt{2-x}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{6}{5}\left(tm\right)\\5x-15=12\sqrt{2-x}\left(1\right)\end{matrix}\right.\)
Vì \(-2\le x\le2\Rightarrow5x-15< 0\Rightarrow\left(1\right)\) vô nghiệm
Vậy phương trình đã cho có nghiệm \(x=\dfrac{6}{5}\)
D
datcoder
CTVVIP
7 tháng 11 2023
Lần sao bạn ấn vào Latex để gõ các công thức như thế nào để câu hỏi được rõ hơn nha. Kí hiệu \(\sum\) ở trên thanh công cụ nhé.
Giải:
ĐKXĐ: \(3-2x\ge0\Leftrightarrow3\ge2x\Leftrightarrow x\le\dfrac{3}{2}\)
\(\sqrt{x^2-6x+9}=3-2x\)
\(\Leftrightarrow x^2-6x+9=\left(3-2x\right)^2\\ \Leftrightarrow x^2-6x+9=9-12x+4x^2\\ \Leftrightarrow3x^2-6x=0\\ \Leftrightarrow3x\left(x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=2\left(ktm\right)\end{matrix}\right.\)
Vậy x = 0
LK
2
20 tháng 9 2021
\(ĐK:x\ge-\dfrac{3}{2}\\ \Leftrightarrow\sqrt{\left(2x-3\right)\left(2x+3\right)}-2\sqrt{2x+3}=0\\ \Leftrightarrow\sqrt{2x+3}\left(\sqrt{2x-3}-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2x+3=0\\\sqrt{2x-3}=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\left(tm\right)\\2x-3=4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\left(tm\right)\\x=\dfrac{7}{2}\left(tm\right)\end{matrix}\right.\)
20 tháng 9 2021
\(\sqrt{4x^2-9}=2\sqrt{2x+3}\left(đk:x\ge\dfrac{3}{2}\right)\)
\(\Leftrightarrow4x^2-9=4\left(2x+3\right)\)
\(\Leftrightarrow4x^2-9=8x+12\)
\(\Leftrightarrow4x^2-8x-21=0\)
\(\Leftrightarrow\left(2x-7\right)\left(2x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\left(tm\right)\\x=-\dfrac{3}{2}\left(ktm\right)\end{matrix}\right.\)
TN
2
22 tháng 9 2021
\(ĐK:x\le-\dfrac{3}{2};\dfrac{3}{2}\le x\\ Pt\Leftrightarrow\sqrt{\left(2x+3\right)\left(2x-3\right)}-2\sqrt{2x+3}=0\\ \Leftrightarrow\sqrt{2x+3}\left(\sqrt{2x-3}-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}\sqrt{2x+3}=0\\\sqrt{2x-3}=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x+3=0\\2x-3=4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\left(tm\right)\\x=\dfrac{7}{2}\left(tm\right)\end{matrix}\right.\)
22 tháng 9 2021
\(\sqrt{4x^2-9}=2\sqrt{2x+3}\) đk \(x\ge\dfrac{3}{2}\)
\(\Leftrightarrow4x^2-9=4\left(2x+3\right)\)
\(\Leftrightarrow4x^2-9=8x+12\)
\(\Leftrightarrow4x^2-8x-21=0\)
\(\Leftrightarrow\left(2x-7\right)\left(2x+3\right)=0\)
\(\left[{}\begin{matrix}x=\dfrac{7}{2}\left(nhận\right)\\x=-\dfrac{3}{2}\left(loại\right)\end{matrix}\right.\)
Vậy S=\(\left\{\dfrac{7}{2}\right\}\)
10 tháng 5 2022
a: |x+9|=2
=>x+9=2 hoặc x+9=-2
=>x=-7 hoặc x=-11
b: |2x-3|=x-3
\(\Leftrightarrow\left\{{}\begin{matrix}x>=3\\\left(2x-3-x+3\right)\left(2x-3+x-3\right)=0\end{matrix}\right.\Leftrightarrow x=3\)
BL
1
NH
2 tháng 3 2023
\(\dfrac{x+3}{x-3}-\dfrac{x}{x+3}=\dfrac{2x^2+9}{x^2-9}\left(x\ne-3;x\ne3\right)\\ < =>\dfrac{\left(x+3\right)^2}{\left(x-3\right)\left(x+3\right)}-\dfrac{x\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}=\dfrac{2x^2+9}{\left(x-3\right)\left(x+3\right)}\)
suy ra
`x^2 +6x+9-x^2 +3x=2x^2 +9`
`<=> 2x^2 - x^2 +x^2 - 6x -3x +9 -9=0`
`<=> 2x^2 -9x=0`
`<=> x(2x-9)=0`
\(< =>\left[{}\begin{matrix}x=0\\2x-9=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=0\left(tm\right)\\x=\dfrac{9}{2}\left(tm\right)\end{matrix}\right.\)
PT
1
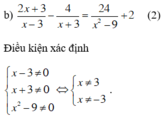
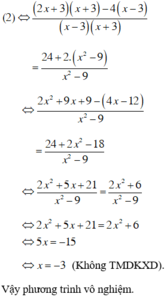
`(2x+3)^2 =` \(\dfrac{9}{121}\)
`=> (2x + 3)^2 =` \(\left(\dfrac{3}{11}\right)^2\)
=> \(\left[{}\begin{matrix}2x+3=\dfrac{3}{11}\\2x+3=-\dfrac{3}{11}\end{matrix}\right.\)
=> \(\left[{}\begin{matrix}2x=\dfrac{3}{11}-3\\2x=-\dfrac{3}{11}-3\end{matrix}\right.\)
=> \(\left[{}\begin{matrix}2x=\dfrac{3}{11}-\dfrac{33}{11}\\2x=-\dfrac{3}{11}-\dfrac{33}{11}\end{matrix}\right.\)
=> \(\left[{}\begin{matrix}2x=-\dfrac{30}{11}\\2x=-\dfrac{36}{11}\end{matrix}\right.\)
=> \(\left[{}\begin{matrix}x=-\dfrac{15}{11}\\x=-\dfrac{18}{11}\end{matrix}\right.\)
Vậy ...
\(\left(2x+3\right)^2=\dfrac{9}{121}\)
\(\left(2x+3\right)^2=\left(\dfrac{3}{11}\right)^2\)
\(2x+3=\dfrac{2}{11}\) hoặc \(2x+3=-\dfrac{2}{11}\)
\(2x=-\dfrac{31}{11}\) hoặc \(2x=-\dfrac{35}{11}\)
\(x=-\dfrac{31}{22}\) hoặc \(x=-\dfrac{35}{22}\)