Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
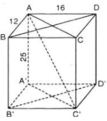
a) ABCD.A’B’C’D’ là hình hộp chữ nhật
⇒ AA’ // CC’, AA’ = CC’
⇒ AA’C’C là hình bình hành
Lại có : AA’ ⊥ (ABCD) ⇒ AA’ ⊥ AC ⇒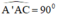 
⇒ Hình bình hành AA’C’C là hình chữ nhật.
Chứng minh tương tự được tứ giác BDD'B' là những hình chữ nhật
b) Áp dụng định lý Pytago:
Trong tam giác vuông ACC’ ta có:
AC’2 = AC2 + CC’2 = AC2 + AA’2
Trong tam giác vuông ABC ta có:
AC2 = AB2 + BC2 = AB2 + AD2
Do đó: AC’2 =AB2 + AD2 + AA’2.
c) Hình hộp chữ nhật được xem như hình lăng trụ đứng.
Diện tích xung quanh:
Sxq = 2.(AB + AD).AA’
= 2.(12 + 16).25
= 1400 (cm2 )
Diện tích một đáy:
Sđ = AB.AD
= 12.16
= 192 (cm2 )
Diện tích toàn phần:
Stp = Sxq + 2Sđ
= 1400 + 2.192
= 1784 (cm2 )
Thể tích:
V = AB.AD.AA’
= 12.16.25
= 4800 (cm3 )
I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
a: Xét ΔABC có AH/AB=AO/AC
nên OH//BC và OH/BC=AH/AB=1/2
b: OH//BC
=>OH//AK
OH=BC/2
=>OH=AD/2=AK
Xét tứ giác AHOK có
OH//AK
OH=AK
góc HAK=90 độ
=>AHOK là hình chữ nhật
Xét tam giác ABC có M; N là trung điểm của Ab;AC nên:
MN//Ac; MN=1/2AC (1)
Xét tam giác ADC có P;Q là trung dime639 của AD; CD nên:
PQ//AC; PQ=1/2AC (2)
Từ (1) và (2) =>MNPQ là hình bình hành
Ta lại có: MQ là đg trung bình của tam giác ABD nên:
MQ//BD
Khi đó: MN//AC
1
Xét tam giác vuông AEH và EBF:
AH=BF (gt)
A=B (gt)
AE=EB (gt)
=>AEH=EBF (2 cạnh góc vuông)
=> EH=EF (2 cạnh tương ứng)
Chứng minh tương tự:
Ta có tam giác AEH=EBF=HGD=FCG
=>HG=GF=FE=EH
=>EFGH là hình thoi
a) BB’ ⊥ A’B’ (ABB’A’ là hình chữ nhật)
BB’ ⊥ B’C’ (BCC’B’ là hình chữ nhật)
=> BB’ ⊥ mp(A’B’C’D’)
=> BB’ ⊥ B’D’ hay
Hình bình hành BDD’B’ có một góc vuông nên là hình chữ nhật
BB’ vuông góc với hai đường thẳng cắt nhau AB và BC
=> BB’ ⊥ mp(ABCD)
c) mp(ABB’A’) chứa BB’ mà BB’⊥ mp(ABCD)
=> mp(ABB’A’) ⊥ mp(ABCD)
a)
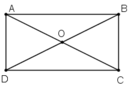
Giả sử ABCD là hình chữ nhật. Gọi O là giao điểm của AC và BD.
Theo tính chất đường chéo của hình chữ nhật ta có; hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.
Vậy: OA = OC và OB= OD
Do đó, O là tâm đối xứng của hình chữ nhật đó.
b)
Áp dung tính chất: Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.
ABCD là hình chữ nhật
⇒ ABCD là hình thang cân (hai đáy AB và CD)
⇒ Đường thẳng đi qua trung điểm AB và CD là trục đối xứng ABCD.
Tương tự vậy: ABCD cũng là hình thang cân với hai đáy AD và BC
⇒ Đường thẳng đi qua trung điểm AD và BC là trục đối xứng của ABCD.
Vậy ta có điều phải chứng minh.
a] Để chứng minh AF // BD, ta cần chứng minh tỉ số đồng dạng giữa các cặp cạnh tương ứng của hai tam giác ACF và BDE. Ta có:
AC/BD = AD/BE (vì AF // BD) AC/AD = BE/BD (vì AM // BD và BN // BD)
Từ hai tỉ số trên, ta có:
AC/AD = BE/BD
Vậy, ta đã chứng minh được AF // BD.
b] Để chứng minh E là trung điểm CF, ta cần chứng minh CE = EF và CF // AB. Ta có:
CE = AM (vì CE // AM và AC // BD) EF = BN (vì EF // BN và AC // BD)
Vậy, ta đã chứng minh được E là trung điểm CF.
1:ΔABC cân tại A
mà AH là đường trung tuyến
nên AH\(\perp\)BC tại H
Xét tứ giác AHCD có
O là trung điểm chung của AC và HD
=>AHCD là hình bình hành
Hình bình hành AHCD có \(\widehat{AHC}=90^0\)
nên AHCD là hình chữ nhật
2: AHCD là hình chữ nhật
=>AD//HC và AD=HC
Ta có: AD//HC
=>AD//HB
Ta có: AD=CH
mà CH=HB
nên AD=HB
Xét tứ giác ADHB có
AD//HB
AD=HB
Do đó: ADHB là hình bình hành
3: \(CH=\dfrac{CB}{2}=3\left(cm\right)\)
AHCD là hình chữ nhật
=>\(S_{AHCD}=AH\cdot HC=4\cdot3=12\left(cm^2\right)\)