cứu mik với, mik cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì OA là tia phân giác của xOC => xOA=AOC=12.xOCxOA=AOC=12.xOC (1)
Vì OB là tia phân giác của COy => COB=BOy=12.COyCOB=BOy=12.COy (2)
Từ (1) và (2) => xOA+BOy=AOC+BOC=12.xOC+12.COyxOA+BOy=AOC+BOC=12.xOC+12.COy
=> xOA+BOy=AOB=12.(xOC+COy)xOA+BOy=AOB=12.(xOC+COy)
=> 90o=12.xOy90o=12.xOy
=> xOy=90:12xOy=90:12
=> xOy = 90.2 = 180 => là góc bẹt
=> Ox và Oy là 2 tia đối nhau
Vậy Ox và Oy là 2 tia đối nhau
hihi

Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC.
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC (như hình vẽ)
(H ∈ tia AB, I ∈ BC, K ∈ tia AC)
Theo định lí 1: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.
Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài )
MI = MK ( Vì M thuộc phân giác của góc C ngoài )
Suy ra: MH = MK (cùng bằng MI)
Dựa vào định lí 2: Điểm nằm bên trong góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.
⇒ M thuộc phân giác của góc BAC (đpcm).

1.tính diện tích hình tam giác:ta lấy độ dài đáy nhân chiều cao rồi đóng mở ngoặc chia cho 2
2.tính diện tích hình thang:ta lấy chiều dài cộng chiều rộng,đóng mở ngoặc rồi nhân với 2 và nhân chiều cao.
3.tính diện tích hình tròn:ta lấy bán kính nhân bán kính và nhân 3,14.
hết

- Thứ tự sắp xếp là 5, 1, 2, 4, 3
Tam giác AMB và tam giác EMC có
MB = MC (gt)
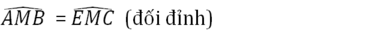
MA = ME (gt)
Do đó ΔAMB = ΔEMC (c.g.c)


A B C O E H Y F
câu a
có OE vuông góc với bc =>tam giác OEC vuông tại E
có OH vuông góc với AC => tam giác OHC vuông tại H
xét tam giác vuông OEC và tam giác vuông OHC
có : góc ECO = góc HCO( OC là phân giác của góc C )
OC là cạnh chung
=> tam giác vuông ECO = tam giác vuông HCO ( trườnghợp đặc biệt của tam giác vuông : cạnh huyền - góc nhọn )
câu b
có tam giác vuông OEC = tam giác vuông HCO (chứng minh ở câu a )
=> EC = HC ( 2 cạnh tương ứng )
xét tam giác ECY và tam giác YCH
có : EC = EH( chứng minh trên )
góc ECY= góc YCH (phan giác góc C )
CY cạnh chung
=> tam giác ECY = tam giác YCH (trường hợp : c-g-c)
=> EY = YH ( 2 cạnh tương ứng ) => Y là trungđiểm của EH (1)
=> góc EYC = góc HYC ( 2 góc tương ứng )
Mà góc EYC + góc HYC = 180 độ ( 2 góc kề bù )
mà góc EYC = góc HYC (chứng minh trên ) => góc EYC =góc HYC = 900 => CY vuông với EH tại Y hay CO cũng vuông góc với EH (2)
từ (1) và (2) => OC làđường trung trực của HE
câu c
có tam giác vuông OEC = tam giác vuông OHC (chứng minh ở câu a )
=> OE = OH( 2 cạnh tương ứng )
có OFvuông góc với AB => tam giác BFO vuông tại F
có OE vuông góc với BC => tam giác OBE vuông tại E
xét tam giác vuông BFO và tam giác vuông BEO
có :góc FBO = góc EBO( fân giác của góc B)
Bo là cạnh chung
=> tam giác vuông FBO =tam giác vuông EBO ( trường hợp đặt biệt của tam giác cuông : cạnh huyền - góc nhọn)
=> OF= OE ( 2 cạnh tương ứng )
mà OE=OH
=> OF = OH => điều phải chứng minh (câu c ý 1 )
câu c ý 2 :
xét tam giá vuông OFA và tamgiác vuông OHA
có:FO=OH ( chứng minh trên)
OA là cạnh chung
=>tam giác vuông FOA = tam giác vuông OHA ( trường hợp đặc biệt của tam giác vuông : cạnh huyền - cạnh góc vuông )
=> góc AOF = góc AOH ( 2 góc tương ứng )
câu d
lát làm nha ,giờ mk có việc r,có j ib mk mk làm nốt ,
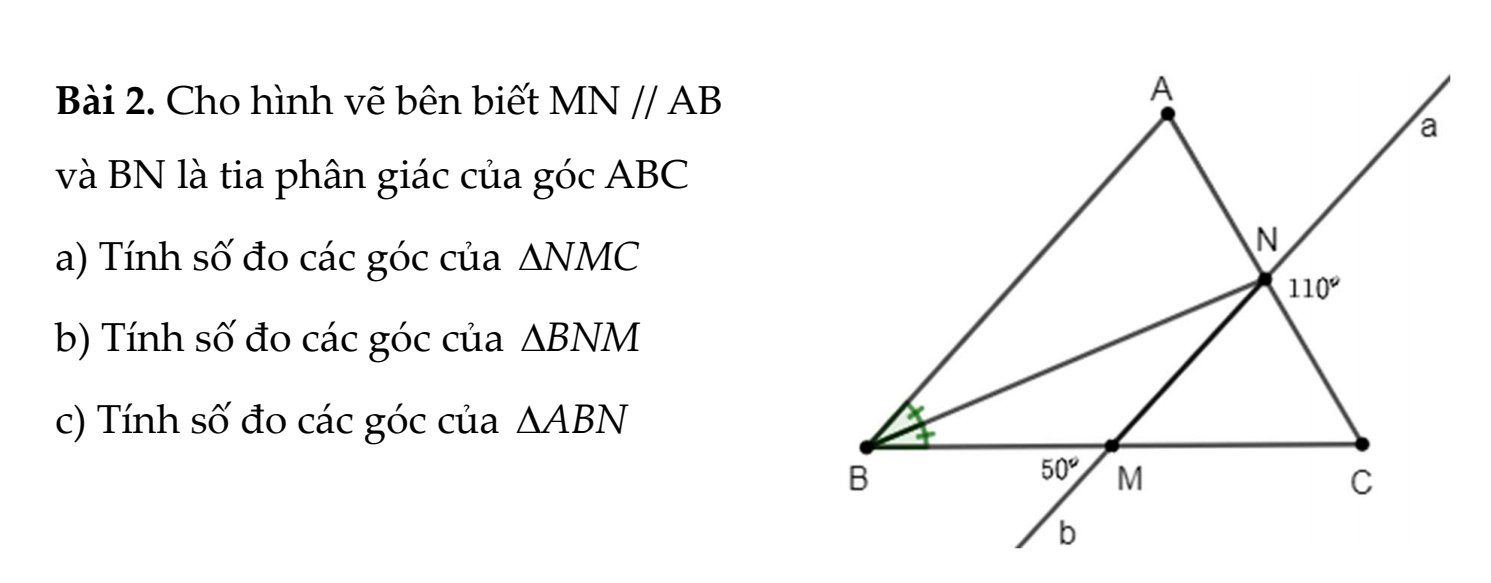
a: Ta có: \(\widehat{bMB}=\widehat{NMC}\)(hai góc đối đỉnh)
mà \(\widehat{bMB}=50^0\)
nên \(\widehat{NMC}=50^0\)
Ta có: \(\widehat{MNC}+\widehat{aNC}=180^0\)(hai góc kề bù)
=>\(\widehat{MNC}+110^0=180^0\)
=>\(\widehat{MNC}=70^0\)
Xét ΔMNC có \(\widehat{NMC}+\widehat{MNC}+\widehat{C}=180^0\)
=>\(\widehat{C}+50^0+70^0=180^0\)
=>\(\widehat{C}=60^0\)
b: Ta có: \(\widehat{NMB}+\widehat{NMC}=180^0\)(hai góc kề bù)
=>\(\widehat{NMB}+50^0=180^0\)
=>\(\widehat{NMB}=130^0\)
Ta có: MN//AB
=>\(\widehat{CMN}=\widehat{CBA}\)(hai góc đồng vị)
=>\(\widehat{CBA}=50^0\)
BN là phân giác của góc CBA
=>\(\widehat{NBM}=\dfrac{\widehat{ABC}}{2}=25^0\)
Xét ΔNMB có \(\widehat{NMB}+\widehat{BNM}+\widehat{NBM}=180^0\)
=>\(\widehat{MNB}=180^0-130^0-25^0=25^0\)
c: BN là phân giác của góc CBA
=>\(\widehat{ABN}=\dfrac{\widehat{ABC}}{2}=25^0\)
Xét ΔABC có \(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0\)
=>\(\widehat{BAN}+60^0+50^0=180^0\)
=>\(\widehat{BAN}=70^0\)
Xét ΔBAN có \(\widehat{BAN}+\widehat{ABN}+\widehat{ANB}=180^0\)
=>\(\widehat{ANB}=180^0-75^0-25^0=85^0\)