-4x3+4x2+x-1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
F
0
2 tháng 8 2021
Bài 1:
a) Thay m=3 vào (1), ta được:
\(x^2-4x+3=0\)
a=1; b=-4; c=3
Vì a+b+c=0 nên phương trình có hai nghiệm phân biệt là:
\(x_1=1;x_2=\dfrac{c}{a}=\dfrac{3}{1}=3\)
2 tháng 8 2021
Bài 2:
a) Thay m=0 vào (2), ta được:
\(x^2-2x+1=0\)
\(\Leftrightarrow\left(x-1\right)^2=0\)
hay x=1
25 tháng 1 2022
4x - 20 = 0 <=> x =20/4 = 5
x - 5 = 3 - x <=> 2x = 8 <=> x = 4
HT
0
HT
2
2
12 tháng 5 2022
`1-D`
Vì `7-2x=0` có dạng của ptr bậc nhất một ẩn `ax+b=0` trong đó `a=-2 \ne 0`
_________________________________________________
`2-C`
Vì `-x+1 < 0` có dạng bất ptr bậc nhất một ẩn `ax+b < 0` và `a=-1 \ne 0`
__________________________________________________
`3-A`
`4x-10 > x+2`
`<=>4x-x > 2+10`
`<=>3x > 12`
`<=>x > 4`
_________________________________________________
`4-C`
Vì tỉ số đồng dạng của `2` hai tam giác đồng dạng bằng tỉ số của `2` đường cao tương ứng của `2` tam giác đồng dạng đó
DA
0
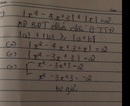
\(-4x^3+4x^2+x-1\)
\(=-4x^2\left(x-1\right)+\left(x-1\right)\)
\(=\left(x-1\right)\left(1-4x^2\right)=\left(x-1\right)\left(1-2x\right)\left(1+2x\right)\)
\(-4x^3+4x^2+x-1\\ =-4x^2\left(x-1\right)+\left(x-1\right)\\ =\left(x-1\right)\left(1-4x^2\right)\\ =\left(x-1\right)\left[1^2-\left(2x\right)^2\right]\\ =\left(x-1\right)\left(1-2x\right)\left(1+2x\right)\)