(4x+12)×(x+5)=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 3 2021
Không biết em có làm sai không:
ĐKXĐ: \(x,y\ge0\).
Đặt 2x = a; 3y = b.
HPT trở thành:
\(\left\{{}\begin{matrix}\left(\sqrt{5}\right)^a-\left(\sqrt{5}\right)^b+\left(a-b\right)\left(ab+12\right)=0\\a^2+b^2=16\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2+b^2=16\\\left(\sqrt{5}\right)^a-\left(\sqrt{5}\right)^b+\left(b-a\right)\left(a^2+b^2\right)+a^3-b^3+12\left(a-b\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2+b^2=16\\\left(\sqrt{5}\right)^a+a^3-4a=\left(\sqrt{5}\right)^b+b^3-4b=0\left(1\right)\end{matrix}\right.\).
Giả sử \(a\ge b\Rightarrow\left(\sqrt{5}\right)^a\ge\left(\sqrt{5}\right)^b\). Mà \(\left(a^3-4a\right)-\left(b^3-4b\right)=\left(a-b\right)\left(a^2+ab+b^2-4\right)\ge0\) nên VT(1) \(\ge\) VP(1).
Do đẳng thức xảy ra nên ta có a = b. Thay vào ta tìm được a = b = \(2\sqrt{2}\) nên \(x=\sqrt{2};y=\dfrac{2\sqrt{2}}{3}\).
HT
15 tháng 3 2021
\(\left\{{}\begin{matrix}\left(\sqrt{5}\right)^{2x}-\left(\sqrt{5}\right)^{3y}=\left(3y-2x\right)\left(6xy+12\right)\left(1\right)\\4x^2+9y^2=16\left(2\right)\end{matrix}\right.\)
\(\left(2\right)\Rightarrow4x^2+9y^2-4=12\) the vo (1)
\(\Rightarrow\left(\sqrt{5}\right)^{2x}-\left(\sqrt{5}\right)^{3y}=\left(3y-2x\right)\left(6xy+4x^2+9y^2-4\right)\)
\(\Leftrightarrow\left(\sqrt{5}\right)^{2x}-\left(\sqrt{5}\right)^{3y}=27y^3-8x^3-12y+8x\)
\(\Leftrightarrow\left(\sqrt{5}\right)^{2x}+\left(2x\right)^3-4.\left(2x\right)=\left(\sqrt{5}\right)^{3y}+\left(3y\right)^3-4.\left(3y\right)\left(3\right)\)
Xét hàm số \(f\left(t\right)=\left(\sqrt{5}\right)^{2t}+\left(2t\right)^3-4.2t\) đồng biến trên R
\(\Rightarrow\left(3\right):f\left(2x\right)=f\left(3y\right)\Leftrightarrow\left\{{}\begin{matrix}2x=3y\\4x^2+9y^2=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\sqrt{2}\\y=\dfrac{2\sqrt{2}}{3}\end{matrix}\right.\)
12 tháng 5 2023
1:
a: =>3x=6
=>x=2
b: =>4x=16
=>x=4
c: =>4x-6=9-x
=>5x=15
=>x=3
d: =>7x-12=x+6
=>6x=18
=>x=3
2:
a: =>2x<=-8
=>x<=-4
b: =>x+5<0
=>x<-5
c: =>2x>8
=>x>4
Y
12 tháng 4 2022
\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)
\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)
\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)
\(\Leftrightarrow x^2-9-x^2+3x=0\)
\(\Leftrightarrow3x-9=0\)
\(\Leftrightarrow3x=9\)
\(\Leftrightarrow x=3\left(n\right)\)
Vậy \(S=\left\{3\right\}\)
Y
12 tháng 4 2022
\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)
\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)
\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)
\(\Leftrightarrow12x-9-12x+20+2x-7>0\)
\(\Leftrightarrow2x+4>0\)
\(\Leftrightarrow2x>-4\)
\(\Leftrightarrow x>-2\)
H
23 tháng 2 2023
`a,x^2 +4x-5=0`
`<=> x^2-x+5x-5=0`
`<=> x(x-1)+5(x-1)=0`
`<=>(x-1)(x+5)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-5\end{matrix}\right.\)
`b, x^2 -x-12=0`
`<=> x^2 +3x-4x-12=0`
`<=>(x^2+3x)-(4x+12)=0`
`<=>x(x+3)-4(x+3)=0`
`<=>(x+3)(x-4)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x-4=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=4\end{matrix}\right.\)
`c, (2x-7)^2 - 6(2x-7)(x-3)=0`
`<=>(2x-7)(2x-7 -6x+18)=0`
`<=>(2x-7) ( -4x+11)=0`
\(\Leftrightarrow\left[{}\begin{matrix}2x-7=0\\-4x+11=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=7\\-4x=-11\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=\dfrac{11}{4}\end{matrix}\right.\)
23 tháng 2 2023
a: =>(x+5)(x-1)=0
=>x=1 hoặc x=-5
b: =>(x-4)(x+3)=0
=>x=4 hoặc x=-3
c: =>(2x-7)(2x-7-6x+18)=0
=>(2x-7)(-4x+11)=0
=>x=11/4 hoặc x=7/2
5 tháng 9 2023
a: ĐKXĐ: x>=3
Sửa đề: \(\sqrt{4x-12}-\sqrt{9x-27}+\sqrt{\dfrac{25x-75}{4}}-3=0\)
=>\(2\sqrt{x-3}-3\sqrt{x-3}+\dfrac{5}{2}\sqrt{x-3}-3=0\)
=>\(\dfrac{3}{2}\sqrt{x-3}=3\)
=>\(\sqrt{x-3}=2\)
=>x-3=4
=>x=7(nhận)
b: ĐKXĐ: x>=0
\(\dfrac{\sqrt{x}-2}{\sqrt{x}+1}< =-\dfrac{3}{4}\)
=>\(\dfrac{\sqrt{x}-2}{\sqrt{x}+1}+\dfrac{3}{4}< =0\)
=>\(\dfrac{4\sqrt{x}-8+3\sqrt{x}+3}{4\left(\sqrt{x}+1\right)}< =0\)
=>\(7\sqrt{x}-5< =0\)
=>\(\sqrt{x}< =\dfrac{5}{7}\)
=>0<=x<=25/49
c: ĐKXĐ: x>=5
\(\sqrt{9x-45}-14\sqrt{\dfrac{x-5}{49}}+\dfrac{1}{4}\sqrt{4x-20}=3\)
=>\(3\sqrt{x-5}-14\cdot\dfrac{\sqrt{x-5}}{7}+\dfrac{1}{4}\cdot2\cdot\sqrt{x-5}=3\)
=>\(\dfrac{3}{2}\sqrt{x-5}=3\)
=>\(\sqrt{x-5}=2\)
=>x-5=4
=>x=9(nhận)
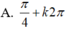
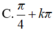
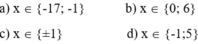
\(\left(4x+12\right)\left(x+5\right)=0\\ \Rightarrow\left[{}\begin{matrix}4x+12=0\\x+5=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}4x=-12\\x=-5\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=-3\\x=-5\end{matrix}\right.\)
Vậy: \(x\in\left\{-3;-5\right\}\)
(4x+12)(x+5)=0
=>4(x+3)(x+5)=0
=>(x+3)(x+5)=0
=>\(\left[{}\begin{matrix}x+3=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-5\end{matrix}\right.\)