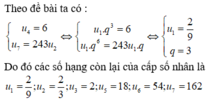Tìm chữ số tc của 243^5^6^7
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



2436=2434+2=2434.2432
=.....1 . 59049
=.....9
Vậy 2436 có chữ số tận cùng là 9


a) \(A=7^{243}\)
Để ý \(7^2=49\)và \(7^4=49^2\)có tận cùng là 1. Vậy \(7^{4k}\)có tận cùng là 1.
243=60x4 +3 nên \(A=7^{243}\)có tận cùng giống với \(7^3=49\cdot7\)
A có tận cùng là 3.
b) \(B=9^{315}\)
Tương tự, B có tận cùng là 9.
c) \(C=13^{131}\)có tận cùng là 7.

+các thừa số 5 trong 100!(khi phân tích ra các thừa số chia hết cho 5) là:
\(\frac{100}{5}\)+\(\frac{100}{25}\)=24(thưà số)
Các thừa số 2 có trong 100! là:
\(\frac{100}{2}+\frac{100}{4}+\left[\frac{100}{8}+\frac{100}{16}+\frac{100}{32}+\frac{100}{64}\right]\)
=50+25+12+6+3+1
=97(số)
Tích của mỗi cặp thừa số 2 và 5 tận cùng bằng 1 chữ số 0.Do đó 100! có tc =24 cs 0
:D

Chọn D.
Gọi cấp số nhân đó là (un), n = 1,7 ¯ . Theo đề bài ta có :
u 4 = 6 u 7 = 243 u 2 ⇔ u 1 . q 3 = 6 u 1 . q 6 = 243 u 1 . q ⇔ u 1 = 2 9 q = 3
Do đó các số hạng còn lại của cấp số nhân là
u 1 = 2 9 ; u 2 = 2 3 ; u 3 = 2 ; u 5 = 18 ; u 6 = 54 ; u 7 = 162