Câu hỏi bạn : " I want to be a famous doctor "
Chứng tỏ rằng: ![]() (n ∈ N) là phân số tối giản
(n ∈ N) là phân số tối giản
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi a,a+1,a+2 là 3 số TN liên tiếp
Theo đề :
a + a + 1 + a + 2 <=> ( a + a + a ) + ( 1 + 2 )
<=> 3a + 3 \(⋮\)3
Vậy tổng ba số TN liên tiếp chia hết cho 3
Gọi 3 số tự nhiên liên tiếp là : a ; a + 1 ; a + 2 với a ∈ N .
Tổng của ba số là :
a + ( a + 1 ) + ( a + 2 ) = a + a + 1 + a + 2
= 3a + 3
Vì 3a = 3 . 3 . 3 . a = 3a + 3 ⋮ 3 từ một số .
Vậy tổng của ba số tự nhiên liên tiếp là một số chia hết cho 3 .

Đặt \(d=\left(n+1,3n+2\right)\).
Suy ra \(\hept{\begin{cases}n+1⋮d\\3n+2⋮d\end{cases}}\Rightarrow3\left(n+1\right)-\left(3n+2\right)=1⋮d\Rightarrow d=1\).
Do đó ta có đpcm.
Đặt \(d=\left(2n+1,4n+3\right)\).
Suy ra \(\hept{\begin{cases}2n+1⋮d\\4n+3⋮d\end{cases}}\Rightarrow\left(4n+3\right)-2\left(2n+1\right)=1⋮d\Rightarrow d=1\).
Do đó ta có đpcm.

Đặt d = ƯCLN( 14n + 3, 21n + 5 ) ( d ∈ N* )
Ta có: 14n + 3 ⋮ d và 21n + 5 ⋮ d
⇒ 3( 14n + 3 ) ⋮ d và 2( 21n + 5 ) ⋮ d ⇒ 42n + 9 ⋮ d và 42n + 10 ⋮ d
⇒ ( 42n + 9 ) – ( 42n + 10 ) ⋮ d ⇒ 1 ⋮ d . Do đó d = 1
Vậy 14 n + 3 21 n + 5 là phân số tối giản

Đặt d = ƯCLN( 14n + 3, 21n + 5 ) ( d ∈ N* )
Ta có: 14n + 3 ⋮ d và 21n + 5 ⋮ d
⇒ 3( 14n + 3 ) ⋮ d và 2( 21n + 5 ) ⋮ d ⇒ 42n + 9 ⋮ d và 42n + 10 ⋮ d
⇒ ( 42n + 9 ) – ( 42n + 10 ) ⋮ d ⇒ 1 ⋮ d . Do đó d = 1
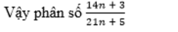 là phân số tối giản.
là phân số tối giản.

Gọi \(ƯCLN\left(3n+1;3n+4\right)=d\)
\(\Rightarrow\)\(\hept{\begin{cases}3n+1⋮d\\3n+4⋮d\end{cases}}\)
\(\Rightarrow\)\(\left(3n+1\right)-\left(3n+4\right)⋮d\)
\(\Rightarrow\)\(\left(-3\right)⋮d\)
\(\Rightarrow\)\(d\inƯ\left(-3\right)=\left\{1;-1;3;-3\right\}\)
Lại có :
\(3n⋮3\)\(;\)\(3n⋮\left(-3\right)\)
\(\Rightarrow\)\(3n+1\) không chia hết cho \(3\) và \(-3\)
\(\Rightarrow\)\(ƯCLN\left(3n+1;3n+4\right)=\left\{1;-1\right\}\)
Vậy \(\frac{3n+1}{3n+4}\) là phân số tối giản với mọi \(n\inℕ\)
Chúc bạn học tốt ~

Để chứng minh 12 n + 1 30 n + 2 là phân số tối giản (n ∈ N), ta cần chứng phân số này có tử và mẫu là hai số nguyên tố cùng nhau (ước chung lớn nhất của hai số đó bằng 1).
Gọi d là ước chung của 12n + 1 và 30n + 2 (n ∈ N)


Gọi UCLN(2n + 3; 4n + 5) là d (d thuộc N*)
=> 2n + 3 chia hết cho d => 4n + 6 chia hết cho d => 4n + 5 + 1 chia hết cho d
và 4n + 5 chia hết cho d
=> 1 chia hết cho d
=> d = 1 (Vì d thuộc N*)
=> UWCLN(2n + 3; 4n + 5) = 1
=> 2n + 3/4n + 5 là phân số tối giản với mọi số tự nhiên n
Vậy,........
Vào coppy
Gọi d là ước chung của n + 3 và 2n + 5 với d ∈ N
=> n + 3 ⋮ d và 2n + 5 ⋮ d
=> (n + 3) - (2n + 5) ⋮d => 2(n + 3) - (2n + 5) ⋮ d <=> 1 ⋮d => d = 1 ∈ N
=> ƯC( n + 3 và 2n + 5) = 1
=> ƯCLN (n + 3 và 2n + 5) = 1 => (n ∈ N) là phân số tối giản.
(n ∈ N) là phân số tối giản.
P/S : Đây chỉ là ý của mk thôi nha