
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

M
9 tháng 10 2019
TL :
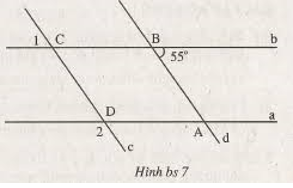
a) Vẽ thêm các tia đối của các tia Dm, Cp, Bq và An.
Vẽ thêm các đường phân giác Ds và Ar của góc ∠D và ∠A.
Khi đó chứng minh được Cp song song với Ds.
Tương tự chứng minh được Ar song song với Dm.
Từ đó suy ra được: An // Cp và Dm // Bq.
b) Sử dụng tính chất tia phân giác của hai góc bù nhau có được Ds, Dm vuông góc với nhau.
Từ đó suy ra được: An vuông góc với Bq.
Hok tốt

a: Ta có: \(\widehat{xBy}=\widehat{xAz}\)(hai góc đồng vị)
mà hai góc này là hai góc ở vị trí đồng vị
nên By//Az
b: AC là phân giác của góc xAz
=>\(\widehat{xAC}=\widehat{zAC}=\dfrac{\widehat{xAz}}{2}=30^0\)
=>\(\widehat{BAC}=30^0\)
Ta có: \(\widehat{CBA}+\widehat{CBx}=180^0\)(hai góc kề bù)
=>\(\widehat{CBA}+60^0=180^0\)
=>\(\widehat{CBA}=120^0\)
Xét ΔBAC có \(\widehat{BAC}+\widehat{CBA}+\widehat{ACB}=180^0\)
=>\(\widehat{ACB}+30^0+120^0=180^0\)
=>\(\widehat{ACB}=30^0\)
c: BD là phân giác của góc yBA
=>\(\widehat{ABD}=\dfrac{\widehat{yBA}}{2}=60^0\)
Xét ΔBDA có \(\widehat{DBA}+\widehat{DAB}=30^0+60^0=90^0\)
nên ΔBDA vuông tại D
=>AC\(\perp\)BD tại D