K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
8 tháng 1 2016
vậy đoạn thẳng ab là 20*3/2=30 m
đoạn thẳng ab là 30*5/4=37.5 m
8 tháng 1 2016
Độ dài của đoạn thằng AB là:
20 : 2/3 = 30 (m)
Độ dài của đoạn thẳng CD là:
30 : 4/5 = 37,5 (m)
Đáp số: 37,5 (m)
CM
24 tháng 7 2017
Đoạn thẳng BC dài số đề-xi-mét là:
8 – 5 = 3 (dm)
Đáp số: b. 3dm.
21 tháng 4 2019
giải
Đổi 1dm6cm=16cm
1dm2cm=12cm
Độ dài đường gấp khúc ABCD là :
13 +12 + 16 = 41 ( cm )
Đ/s : 41 cm
#Dương-Huyền
VT
2
18 tháng 1 2017
Hình ở giữa chính là một hình vuông nên chu vi hình vuông là :
9 * 4 = 36 (cm)
Hai cánh hoa ghép lại thành một hình tròn nên 4 cánh hoa ghép được 2 hình tròn
chu vi của 4 cánh hoa là :
9 * 3,14 = 28,26 (cm )
độ dài sợi dây thép là :
36 + 28,26 = 64,26 9(cm)
Đáp số :64,26 cm
T
4 tháng 4 2022
Bài giải
Hình ở giữa chính là một hình vuông nên chu vi hình vuông là :
9 * 4 = 36 (cm)
Hai cánh hoa ghép lại thành một hình tròn nên 4 cánh hoa ghép được 2 hình tròn
chu vi của 4 cánh hoa là :
9 * 3,14 = 28,26 (cm )
Độ dài sợi dây thép là :
36 + 28,26 = 64,26 9(cm)
Đáp số :64,26 cm
A
21 tháng 6 2019
a) Phân tích bài toán
Giả sử PQ và PR là hai đường xiên kẻ từ P đến d sao cho PQ = PR và\(\widehat{QPR}=60^0\). Gọi H là chân đường vuông góc kẻ từ P đến d. Khi đó ∆PHQ = ∆PHR (cạnh huyền, cạnh góc vuông), suy ra \(\widehat{HPQ}=\widehat{HPR}=30^0\) Từ đó suy ra cách vẽ hai đường xiên PQ và PR.
Kẻ\(PH\perp d\) (H ∈ d). Dùng thước đo góc để vẽ góc HPx bằng 30°. Tia Px cắt d tại điểm Q. Trên d lấy điểm R sao cho HR = HQ. Hai đường xiên PQ và PR lần lượt có hình chiếu trên d là HQ và HR. Do HQ = HR nên PQ = PR.
Hơn nữa\(\widehat{QPR}=2\widehat{HQP}=60^0\)
b) Hướng dẫn
- Tam giác PQR có PQ = PR và \(\widehat{QPR}=60^0\), tam giác PQR là tam giác đều
PQ = 18cm => QR =18cm ; HQ = HR =9cm.
21 tháng 6 2019
Giả sử PQ và PR là hai đường xiên kẻ từ P đến d sao cho PQ = PR và ∠(QPR) = 60°.
Gọi H là chân đường vuông góc kẻ từ P đến d. Khi đó ΔPHQ = ΔPHQ (cạnh huyền, cạnh góc vuông),
suy ra ∠(HPQ) = ∠(HPR) = 30°. Từ đó suy ra cách vẽ hai đường xiên PQ và PR.
Kẻ PH ⊥ d (H ∈ d).
Dùng thước đo góc để vẽ góc HPx bằng 30°.
Tia Px cắt d tại điểm Q. Trên d lấy điểm R sao cho HR = HQ.
Hai đường xiên PQ và PR lần lượt có hình chiếu trên d là HQ và HR.
Do HQ = HR nên PQ = PR.
Hơn nữa ∠(QPR) = 2∠(HPQ) = 60°.
b) Hướng dẫn
- Tam giác PQR có PQ = PR và ∠(QPR) = 60°, tam giác đó là tam giác đều
- PQ = 18cm ⇒ QR =18 cm ; HQ = HR =9 cm
LL
giúp mình câu 4,6,14 ( sách bài tập toán 7-tập 1) phần hình học chương 1
1
HN
21 tháng 6 2017
Bài 6:
A P M N Q 33 o
a) \(\widehat{MAP}=\widehat{NAQ}\) (hai góc đối đỉnh)
Mà \(\widehat{MAP}=33^o\)
Vậy \(\widehat{NAQ}=33^o\).
b) Ta có: \(\widehat{MAP}+\widehat{MAQ}=180^o\) (hai góc kề bù)
Mà \(\widehat{MAP}=33^o\)
Nên \(\widehat{MAQ}=180^o-\widehat{MAP}=180^o-33^o=147^o\)
Vậy \(\widehat{MAQ}=147^o.\)
c) Các cặp góc đối đỉnh:
\(\widehat{MAP}\) và \(\widehat{NAQ}\)
\(\widehat{NAP}\) và \(\widehat{MAQ}\).
d) Các cặp góc bù nhau:
\(\widehat{MAP}\) và \(\widehat{NAP}\)
\(\widehat{NAP}\) và \(\widehat{NAQ}\)
\(\widehat{NAQ}\) và \(\widehat{MAQ}\)
\(\widehat{MAQ}\) và \(\widehat{MAP}\).
HH
26 tháng 2 2020
A B C K H I
a) Xét hai Δvuông HBC và ΔKCB
∠BCH = ∠CBK (Δ ABC cân tại A) BC cạnh chung
⇒ ΔHBC = ΔKCB (cạnh huyền, góc nhọn)
⇒ CH = BK
b) Ta có: AB = AC (ΔABC cân tại A) và CH = BK
- Quảng cáo -
AK = AB – BK và AH = AC – CH ⇒ AK = AH
⇒ AK/AB = AH/AC ⇒ KH//BC
c) Kẻ đường cao AI của Δ ABC và xét Δ IAC
ΔHBC có ∠ACI = ∠BCH
⇒ ΔIAC ∽ ΔHBC(g.g) ⇒ AC/BC = IC/HC ⇒ HC = IC.BC / AC = a2/2b
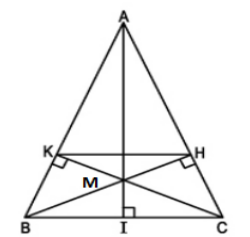
Ta có : \(KH//BC\Rightarrow\frac{KH}{BC}=\frac{AH}{AC}\)
\(\Rightarrow KH=\frac{AH.BC}{AC}=\frac{\left(AC-HC\right).BC}{AC}\)
\(\Rightarrow KH=\left(b-\frac{a^2}{2b}\right)\frac{a}{b}=a-\frac{a^3}{2b^2}\)
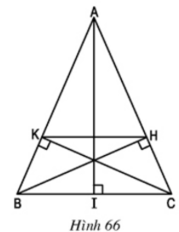
a: Trên tia Ox, ta có: OA<OB
nên A nằm giữa O và B
=>OA+AB=OB
=>AB+2=6
=>AB=4(cm)
b: M là trung điểm của OB
=>\(OM=BM=\dfrac{OB}{2}=3\left(cm\right)\)
Trên tia Ox, ta có: OA<OM(2cm<3cm)
nên A nằm giữaO và M
=>OA+AM=OM
=>AM+2=3
=>AM=1(cm)
a) OA < OB => A nằm giữa O và B
=> AB = OB - OA = 6 - 2 = 4(cm)
b) M là trung điểm của OB =>` OM=MB=1/2OB=1/2*6=3(cm) `
=> AM=AB - MB = 4 - 3 = 1(cm)