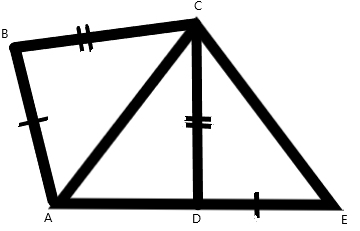
cho tứ giác ABCD có B+D=180 độ và CB=CD trên tia đối của tia DA lấy điểm E sao cho DE=AB
a) chứng minh tam giác ABC = tam giác EDC
b) chứng minh AC là tia phân giác BAD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
YN
18 tháng 11 2021
a, Ta có:
\(\widehat{ADC}+\widehat{ABC}=180^o\left(1\right)\)
\(\widehat{ADC}+\widehat{EDC}=180^o\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\widehat{ABC}=\widehat{EDC}\) (Cùng bù \(\widehat{ADC}\))
Ta xét hai tam giác ABC và EDC:
BC = DC (giả thiết)
AB = DE (giả thiết)
\(\widehat{ABC}=\widehat{EDC}\) (chứng minh trên)
\(\Rightarrow\Delta ABC=\Delta DEC\left(c.g.c\right)\)
b) Ta có: Tam giác ABC = tam giác EDC (chứng minh trên)
=> AC = EC (Hai cạnh tương ứng bằng nhau)
=> Tam giác AEC cân tại A
\(\Rightarrow\widehat{CAE}=\widehat{CEA}\left(3\right)\)
Ta có: \(\widehat{CEA}=\widehat{CAB}\left(4\right)\)
Từ (3) và (4) \(\Rightarrow\widehat{CAE}=\widehat{CAB}\)
=> AC là tia phân giác của \(\widehat{DAB}\)
20 tháng 7 2016
Bạn tự vẽ hình nhé!
a, (Mk nghĩ đề là góc B+D=180o)
Xét tam giác ABC và EDC có:
AB=DE (gt)
DC=BC (gt)
góc EDC=ABC = (180o- ADC)
=> tam giác ABC=EDC (c.g.c)
b, Tam giác ABC=EDC => AC=EC
=> tam giác ACE cân tại C=> góc DAC=DEC (1)
Mặt khác hai tam giác trên bằng nhau => góc DEC=BAC (2)
Từ (1) và (2) => góc DAC=BAC
=> AC là pg góc A
20 tháng 6 2021
ý a, là chứng minh tam giác ABC=tam giác EDC hả?
a,theo giả thiết thì \(\left\{{}\begin{matrix}\angle\left(B\right)+\angle\left(ADC\right)=180^0\\CB=CD,DE=AB\left(1\right)\end{matrix}\right.\)
mà \(\angle\left(EDC\right)+\angle\left(ADC\right)=180^0\)(kề bù)
\(=>\angle\left(B\right)=\angle\left(EDC\right)\)(2)
từ(1)(2)\(=>\Delta ABC=\Delta EDC\left(c.g.c\right)\)
b,do \(\Delta ABC=\Delta EDC\)(cminh tại ý a)\(=>AC=CE\)=>\(\Delta ACE\) cân tại C
\(=>\angle\left(CAD\right)=\angle\left(CED\right)\left(\right)\left(3\right)\)
do \(\Delta ABC=\Delta EDC=>\angle\left(BAC\right)=\angle\left(CED\right)\left(4\right)\)
(3)(4)\(=>\angle\left(CAD\right)=\angle\left(BAC\right)\)=>AC là phân giác góc A
31 tháng 12 2021
2: Xét tứ giác ABDE có
C là trung điểm của BE
C là trung điểm của AD
Do đó: ABDE là hình bình hành
Suy ra: AB//DE
21 tháng 12 2021
a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
21 tháng 12 2021
b, Ta có : góc BAD = góc BED=90 độ (hai góc tương ứng)
=> góc BED là góc V
Ta có ; DA=DE (hai cạnh tương ứng)
16 tháng 2 2022
a) Xét tam giác ABD và tam giác ACD:
AD chung.
AB = AC (gt).
BD = CD (D là trung điểm của BC).
\(\Rightarrow\Delta ABD=\Delta ACD\left(c-c-c\right).\)
b) Xét tam giác ABC: AB = AC (gt).
\(\Rightarrow\Delta ABC\) cân tại A.
Mà AD là trung tuyến (D là trung điểm của BC).
\(\Rightarrow\) AD là phân giác \(\widehat{BAC}\) (Tính chất tam giác cân).
Xét tam giác MAD và tam giác NAD:
AD chung.
AM = AN (gt).
\(\widehat{MAD}=\widehat{NAD}\) (AD là phân giác \(\widehat{BAC}\)).
\(\Rightarrow\Delta MAD=\Delta NAD\left(c-g-c\right).\)
\(\Rightarrow\) DM = DN (2 cạnh tương ứng).
c) Xét tam giác ADC và tam giác EDB:
DC = DB (D là trung điểm của BC).
AD = ED (gt).
\(\widehat{ADC}=\widehat{EDB}\) (Đối đỉnh).
\(\Rightarrow\Delta ADC=\Delta EDB\left(c-g-c\right).\)
\(\Rightarrow\widehat{CAD}=\widehat{BED}\) (2 góc tương ứng).
\(\Rightarrow\) AC // BE.
Mà \(DK\perp BE\left(gt\right).\)
\(\Rightarrow\) \(DK\perp AC.\left(1\right)\)
Ta có: \(\widehat{AMD}=\widehat{AND}\) \(\left(\Delta MAD=\Delta NAD\right).\)
Mà \(\widehat{AMD}=90^o\left(AM\perp MD\right).\)
\(\Rightarrow\widehat{AND}=90^o.\Rightarrow AC\perp ND.\left(2\right)\)
Từ (1); (2) \(\Rightarrow N;D;K\) thẳng hàng.
a; Ta có: \(\widehat{ADC}+\widehat{ABC}=180^0\)
\(\widehat{ADC}+\widehat{EDC}=180^0\)(hai góc kề bù)
Do đó: \(\widehat{ABC}=\widehat{EDC}\)
Xét ΔABC và ΔEDC có
BC=DC
\(\widehat{ABC}=\widehat{EDC}\)
AB=ED
Do đó: ΔABC=ΔEDC
b: Xét tứ giác ABCD có \(\widehat{ABC}+\widehat{ADC}=180^0\)
nên ABCD là tứ giác nội tiếp
=>\(\widehat{CAD}=\widehat{CBD};\widehat{CAB}=\widehat{CDB}\)
mà \(\widehat{CBD}=\widehat{CDB}\)(ΔCBD cân tại C)
nên \(\widehat{CAD}=\widehat{CAB}\)
=>AC là phân giác của góc BAD
a) Tứ giác ABCD có \(\widehat{B}+\widehat{ADC}=180^o\), mà \(\widehat{ADC}+\widehat{EDC}=180^o\) nên \(\widehat{B}=\widehat{EDC}\)
Xét \(\Delta ABC\) và \(\Delta EDC\) có BC=CD, AB=ED, \(\widehat{B}=\widehat{EDC}\) nên \(\Delta ABC=\Delta EDC\left(c-g-c\right)\)
b) \(\Delta ABC=\Delta EDC\Rightarrow AC=EC\) => \(\Delta ACE\) cân tại C \(\Rightarrow\widehat{CAE}=\widehat{CEA}\Rightarrow\widehat{CAD}=\widehat{CED}\) (1)
\(\Delta ABC=\Delta EDC\Rightarrow\widehat{BAC}=\widehat{CED}\) (2)
Từ (1) và (2) \(\Rightarrow\widehat{CAD}=\widehat{BAC}\)
Do đó CA là phân giác góc BAD