tìm tất cả các cặp x,y thỏa mãn: \(5-x^2-2x=y^2+2y+2\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
GC
4
QD
1
T
27 tháng 2 2019
Viết pt trên thành pt bậc 2 đối với x:
\(2x^2-x\left(y+1\right)-\left(2y-1\right)=0\) (1)
(1) có nghiệm \(\Leftrightarrow\Delta=\left(y+1\right)^2+8\left(2y-1\right)\ge0\)
\(\Leftrightarrow y^2+18y-7\ge0\Leftrightarrow\orbr{\begin{cases}y\le-9-2\sqrt{22}\\y\ge-9+2\sqrt{22}\end{cases}}\)
Ta cần có \(\Delta\) là số chính phương.Tức là:
\(y^2+18y-7=k^2\Leftrightarrow\left(x+9\right)^2-k^2=88\)
\(\Leftrightarrow\left(x+9-k\right)\left(x+9+k\right)=88\)
Gắt gắt,đợi tí nghĩ cách khác xem sao,cách này thử sao nổi -_-
CM
1 tháng 5 2019
Chọn C.
Phương pháp: Đưa bài toán về tìm m để hệ có nghiệm duy nhất.
CM
2 tháng 6 2017
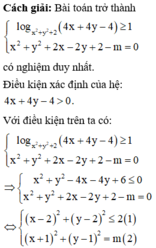
log x 2 + y 2 + 2 4 x + 4 y - 4 ≥ 1
⇔ 4 x + 4 y - 4 ≥ x 2 + y 2 + 2 ⇔ x - 2 2 + y - 2 2 ≤ 2
Đây là tập hợp tất cả các điểm nằm trên và trong đường tròn tâm I(2;2) bán kính ℝ ' = m .
Ta có I I ' = 10 . m nhỏ nhất để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0 thì hai đường tròn nói trên tiếp xúc ngoài
⇒ R + R ' = I I ' ⇔ m + 2 = 10 ⇔ m = 10 - 2 2
Đáp án cần chọn là B
ta có: \(5-x^2-2x=y^2+2y+2.\)
\(\Leftrightarrow\left(y+1\right)^2+\left(x+1\right)^2=5\)
mà \(\left(y+1\right)^2\ge0;\left(x+1\right)^2\ge0\) nên
\(\left(y+1\right)^2+\left(x+1\right)^2=0+5=1+4=2+3\)
TH1: \(\hept{\begin{cases}\left(y+1\right)^2=0\\\left(x+1\right)^2=5\end{cases}\Rightarrow\hept{\begin{cases}y=-1\\x=\sqrt{5}-1\end{cases}}}\)
đến đây tự giải đc rồi nha!
xét xong 3 cặp trên thì kết luận vì x,y có vai trò như nhau nên ta có 6 cặp
Võ Thị Quỳnh Giang sai rồi bạn, bài này mình giải được rồi !