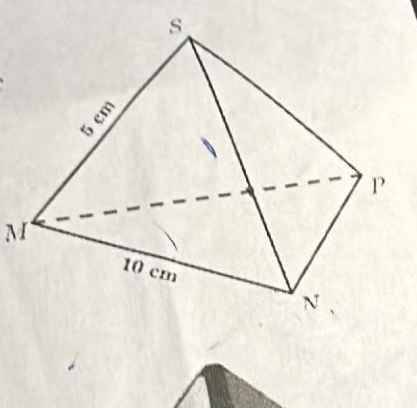
 tính các độ dài các cạnh còn lại của hình chóp . Xác định số đo các của góc tam giác mnp
tính các độ dài các cạnh còn lại của hình chóp . Xác định số đo các của góc tam giác mnp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì Tam giác `MNP` cân tại `M -> MN = MP,` \(\widehat{N}=\widehat{P}\)
Mà `MN= 3 cm, `\(\widehat{N}=60^0\)
`-> MN = MP = 3 cm, `\(\widehat{N}=\widehat{P}=60^0\)
Xét Tam giác `MNP:`
\(\widehat{M}+\widehat{N}+\widehat{P}=180^0\)
`->`\(\widehat{M}+60^0+60^0=180^0\)
`->`\(\widehat{M}=60^0\)
Ta có:
\(\widehat{M}=\widehat{N}=\widehat{P}=60^0\)
`->` \(\text {Tam giác MNP là tam giác đều}\)
`-> MN = MP = NP = 3 cm.`

Hình chóp tam giác đều \(S.DEF\) có:
a) Mặt bên: \(SDE\); \(SDF\); \(SEF\)
Mặt đáy: \(DEF\)
b) Các cạnh bên bằng nhau: \(SE = SF = SD = 5\)cm
Các cạnh đáy bằng nhau: \(ED = EF = DF = 3\)cm
c) Đáy \(DEF\) là tam giác đều nên ba góc ở đáy bằng nhau và bằng \(60^\circ \)

vì tổng 3 góc của 1 tam giá = 180*mà GÓC M=70 *
=>N+M=180*-70*=110*=>GÓC N=M=110*/2=55*

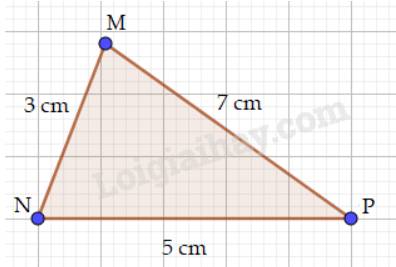
Góc P đối diện với cạnh MN
Góc M đối diện với cạnh NP
Góc N đối diện với cạnh MP.
Ta có: MN < NP < MP nên \(\widehat P < \widehat M < \widehat N\)( định lí)
Vậy sắp xếp các góc của tam giác MNP theo thứ tự từ bé đến lớn là: \(\widehat P;\widehat M;\widehat N\).

Tham khảo:
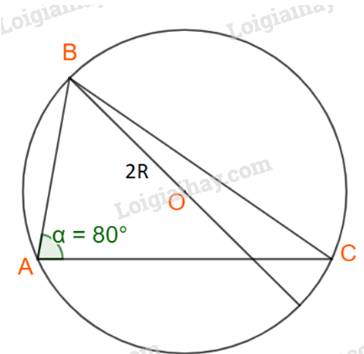
Áp dụng định lí sin cho tam giác ABC ta có:
\(\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = 2R\)
\(\begin{array}{l} \Rightarrow \sin C = \frac{{c.\sin B}}{b} = \frac{{5.\sin {{80}^o}}}{8} \approx 0,6155\\ \Leftrightarrow \widehat C \approx {38^o}\end{array}\)
Lại có: \(\widehat A = {180^o} - \widehat B - \widehat C = {180^o} - {80^o} - {38^o} = {62^o}\)
Theo định lí sin, ta suy ra \(a = \sin A.\dfrac{b}{{\sin B}} = \sin {62^o}\dfrac{8}{{\sin {{80}^o}}} \approx 7,17\)
Và \(2R = \dfrac{b}{{\sin B}} \Rightarrow R = \dfrac{b}{{2\sin B}} = \dfrac{8}{{2\sin {{80}^o}}} \approx 4,062.\)
Vậy tam giác ABC có \(\widehat A = {62^o}\); \(\widehat C \approx {38^o}\); \(a \approx 7,17\) và \(R \approx 4,062.\)
Vì \(S.MNP\) là hình chóp tam giác đều
nên \(SM=SN=SP=5\left(cm\right)\) và \(\triangle MNP\) đều (t/c)
\(\Rightarrow\left\{{}\begin{matrix}MN=NP=PM=10\left(cm\right)\\\widehat{MNP}=\widehat{NPM}=\widehat{PMN}=60^{\circ}\end{matrix}\right.\)