 Giúp mình bài 3 và bài 4 nhé ạ( bằng phương pháp thế trong chương trình mới), chiều tối nay mình đi hc r ạ
Giúp mình bài 3 và bài 4 nhé ạ( bằng phương pháp thế trong chương trình mới), chiều tối nay mình đi hc r ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
ĐKXĐ: \(x\ge\dfrac{1}{2}\)
Ta có: \(\sqrt{5x^2}=2x-1\)
\(\Leftrightarrow5x^2=\left(2x-1\right)^2\)
\(\Leftrightarrow5x^2-4x^2+4x-1=0\)
\(\Leftrightarrow x^2+4x-1=0\)
\(\text{Δ}=4^2-4\cdot1\cdot\left(-1\right)=20\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-4-2\sqrt{5}}{2}=-2-\sqrt{5}\left(loại\right)\\x_2=\dfrac{-4+2\sqrt{5}}{2}=-2+\sqrt{5}\left(loại\right)\end{matrix}\right.\)
Bài 1: Bình phương hai vế lên có giải ra được kết quả. Nhưng phải kèm thêm điều kiện $2x-1\geq 0$ do $\sqrt{5x^2}\geq 0$
PT \(\Leftrightarrow \left\{\begin{matrix} 2x-1\geq 0\\ 5x^2=(2x-1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x^2+4x-1=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2)^2-5=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2-\sqrt{5})(x+2+\sqrt{5})=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x=-2\pm \sqrt{5}\end{matrix}\right.\) (vô lý)
Vậy pt vô nghiệm.

1. hard enough
2. well enough
3. warm enough
4. rich enough
5. enough money
6. enough time
7. strong enough
8. enough French
9. far enough
10. enough chairs
(P/s: nãy h ngồi làm mợt lắm á , tick cho tui nghen (~ ̄▽ ̄)~)

Vì P(x) có nghiệm bằng 2 nên:
P(2) = 0
=> m.2 + 3 = 0
2m = -3
m = \(\frac{-3}{2}\)

Trích mẫu thử :
Cho quỳ tím vào từng mẫu thử :
+ Hóa đỏ : H2SO4 , HCl
+ Hóa xanh : Ba(OH)2
+ Không đổi màu : NaCl
Cho dung dịch Ba(OH)2 ở trên vào 2 mẫu thử làm quỳ tím hóa đỏ :
+ Chất nào xuất hiện kết tủa trắng không tan trong nước : H2SO4
Pt : \(Ba\left(OH\right)_2+H_2SO_4\rightarrow BaSO_4+2H_2O\)
Không hiện tượng : HCl
Chúc bạn học tốt

2:
a: Xét tứ giác OAMD có
\(\widehat{OAM}+\widehat{ODM}=90^0+90^0=180^0\)
=>OAMD là tứ giác nội tiếp
b: Xét (O) có
ΔADC nội tiếp
AC là đường kính
Do đó: ΔADC vuông tại D
=>AD\(\perp\)BC tại D
Xét ΔABC vuông tại A có AD là đường cao
nên \(AD^2=DB\cdot DC\)
Xét (O) có
MA,MD là tiếp tuyến
Do đó: MA=MD
=>\(\widehat{MAD}=\widehat{MDA}\)
mà \(\widehat{MAD}+\widehat{MBD}=90^0\)(ΔADB vuông tại D)
và \(\widehat{MDA}+\widehat{MDB}=\widehat{BDA}=90^0\)
nên \(\widehat{MDB}=\widehat{MBD}\)
=>MD=MB
mà MD=MA
nên MB=MA
=>M là trung điểm của AB
Xét ΔABC có
M,O lần lượt là trung điểm của AB,AC
=>MO là đường trung bình
=>MO//BC
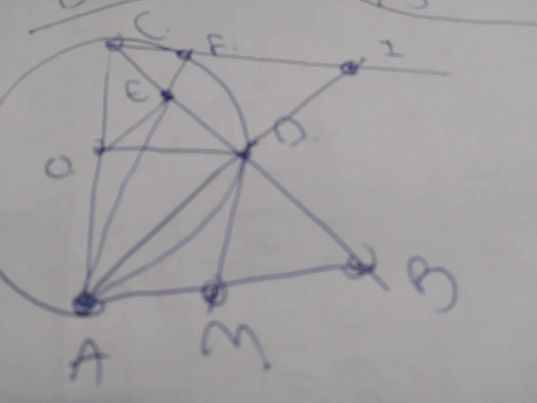
 các bn giúp mình bài 2, bài 3.
các bn giúp mình bài 2, bài 3. các bn giúp mình bài 4 và bài 5 nhé.
các bn giúp mình bài 4 và bài 5 nhé. 



Bài 3:
a: \(\left\{{}\begin{matrix}4x+y=2\\\dfrac{4}{3}x+\dfrac{1}{3}y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2-4x\\\dfrac{4}{3}x+\dfrac{1}{3}\left(2-4x\right)=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=2-4x\\\dfrac{4}{3}x+\dfrac{2}{3}-\dfrac{4}{3}x=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2-4x\\\dfrac{2}{3}=1\left(vôlý\right)\end{matrix}\right.\)
=>Hệ phương trình vô nghiệm
b: \(\left\{{}\begin{matrix}x-y\sqrt{2}=0\\2x+y\sqrt{2}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=y\sqrt{2}\\2y\sqrt{2}+y\sqrt{2}=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3y\sqrt{2}=3\\x=y\sqrt{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}\\x=\dfrac{y\sqrt{2}}{2}=\dfrac{\sqrt{2}}{2}\cdot\sqrt{2}=1\end{matrix}\right.\)
c: \(\left\{{}\begin{matrix}5x\sqrt{3}+y=2\sqrt{2}\\x\sqrt{6}-y\sqrt{2}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\sqrt{2}-5x\sqrt{3}\\x\sqrt{6}-\sqrt{2}\left(2\sqrt{2}-5x\sqrt{3}\right)=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\sqrt{6}-4+5x\sqrt{6}=2\\y=2\sqrt{2}-5x\sqrt{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6x\sqrt{6}=6\\y=2\sqrt{2}-5\sqrt{3}\cdot x\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{1}{\sqrt{6}}=\dfrac{\sqrt{6}}{6}\\y=2\sqrt{2}-5\sqrt{3}\cdot\dfrac{\sqrt{6}}{6}=-\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)
d: \(\left\{{}\begin{matrix}2\left(x+y\right)+3\left(x-y\right)=4\\\left(x+y\right)+2\left(x-y\right)=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+2y+3x-3y=4\\x+y+2x-2y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x-y=4\\3x-y=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=5x-4\\3x-\left(5x-4\right)=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=5x-4\\-2x+4=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=5\cdot\dfrac{-1}{2}-4=-\dfrac{5}{2}-4=-\dfrac{13}{2}\end{matrix}\right.\)