 Giúp hết ạ mình cảm ơn mn nhìu
Giúp hết ạ mình cảm ơn mn nhìu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\Leftrightarrow\sqrt{\left(x-2\right)^2}=7\)
\(\Leftrightarrow\left|x-2\right|=7\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=7\\x-2=-7\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=9\\x=-5\end{matrix}\right.\)
Ta có: \(\sqrt{x^2-4x+4}-5=2\)
\(\Leftrightarrow\left|x-2\right|=7\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=7\\x-2=-7\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=9\\x=-5\end{matrix}\right.\)



Câu 2.
Khối lượng riêng của hòn gạch:
\(D=\dfrac{m}{V}=\dfrac{1,6}{\left(1200-2\cdot192\right)\cdot10^{-6}}\approx1961kg/m^3\)
Trọng lượng riêng của gạch:
\(d=10D\approx19610\left(N/m^3\right)\)
Câu 3.
a)Nếu đứng bằng một chân thì áp suất chiếc giày tác dụng lên mặt sàn:
\(p_1=\dfrac{F}{S_1}=\dfrac{P}{S_1}=\dfrac{600}{100\cdot10^{-4}}=60000Pa\)
b)Nếu đứng bằng một chân thì áp suất mỗi chiếc giày tác dụng lên mặt sàn:
\(p_2=\dfrac{F}{S_2}=\dfrac{P}{S_2}=\dfrac{600}{2\cdot100\cdot10^{-4}}=30000Pa\)
Câu 4.
Áp suất của xe tác dụng lên mặt đường:
\(p=\dfrac{F}{S}=\dfrac{26000}{130\cdot10^{-2}}=20000N/m^2\)
Trọng lượng của người đó: \(P=10m=10\cdot45=450N\)
Áp suất của người tác dụng hai chân lên mặt đất:
\(p'=\dfrac{P}{S'}=\dfrac{450}{200\cdot10^{-2}}=225N/m^2\)
Như vậy \(p>p'\).
Câu 5.
a)Áp lực của máy giặt tác dụng lên sàn:
\(F=p\cdot S=4000\cdot0,3=1200N\)
b)Trọng lượng người đó: \(P=10m=10\cdot65=650N\)
Áp suất của máy giặt đặt trên mặt sàn:
\(p'=\dfrac{P}{S'}=\dfrac{650}{160\cdot10^{-4}}=40625N/m^2\)
Vậy \(p< < < p'\).

Bài 1:
\(a,A=6\sqrt{2}-6\sqrt{2}+2\sqrt{5}=2\sqrt{5}\\ b,B=\dfrac{\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}+\dfrac{\sqrt{2}\left(\sqrt{2}-1\right)}{\sqrt{2}-1}=\sqrt{3}+\sqrt{2}\\ c,=2\sqrt{3}-6\sqrt{3}+15\sqrt{3}-4\sqrt{3}=7\sqrt{3}\\ d,=1+6\sqrt{3}-\sqrt{3}-1=5\sqrt{3}\\ e,=4\sqrt{2}+\sqrt{2}-6\sqrt{2}+3\sqrt{2}=2\sqrt{2}\)
Bài 2:
\(a,ĐK:x\ge\dfrac{3}{2}\\ PT\Leftrightarrow\sqrt{2x-3}=5\Leftrightarrow2x-3=25\Leftrightarrow x=14\\ b,PT\Leftrightarrow x^2=\sqrt{\dfrac{98}{2}}=\sqrt{49}=7\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{7}\\x=-\sqrt{7}\end{matrix}\right.\\ c,ĐK:x\ge3\\ PT\Leftrightarrow\sqrt{x-3}\left(\sqrt{x+3}+1\right)=0\\ \Leftrightarrow\sqrt{x-3}=0\left(\sqrt{x+3}+1>0\right)\\ \Leftrightarrow x=3\\ d,ĐK:x\ge1\\ PT\Leftrightarrow2\sqrt{x-1}-\sqrt{x-1}+3\sqrt{x-1}=4\\ \Leftrightarrow\sqrt{x-1}=1\Leftrightarrow x=2\left(tm\right)\\ e,PT\Leftrightarrow2x-1=16\Leftrightarrow x=\dfrac{17}{2}\\ f,PT\Leftrightarrow\left|2x-1\right|=\sqrt{3}-1\Leftrightarrow\left[{}\begin{matrix}2x-1=\sqrt{3}-1\\2x-1=1-\sqrt{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{3}}{2}\\x=\dfrac{2-\sqrt{3}}{2}\end{matrix}\right.\)
Bài 3:
\(a,Q=\dfrac{1+5}{3-1}=3\\ b,P=\dfrac{x+\sqrt{x}-6+x-2\sqrt{x}-3-x+4\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ P=\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}}{\sqrt{x}-3}\\ c,M=\dfrac{\sqrt{x}}{\sqrt{x}-3}\cdot\dfrac{3-\sqrt{x}}{\sqrt{x}+5}=\dfrac{-\sqrt{x}}{\sqrt{x}+5}\)
Vì \(-\sqrt{x}\le0;\sqrt{x}+5>0\) nên \(M< 0\)
Do đó \(\left|M\right|>\dfrac{1}{2}\Leftrightarrow M< -\dfrac{1}{2}\Leftrightarrow-\dfrac{\sqrt{x}}{\sqrt{x}+5}+\dfrac{1}{2}< 0\)
\(\Leftrightarrow\dfrac{2\sqrt{x}-\sqrt{x}-5}{2\left(\sqrt{x}+5\right)}< 0\Leftrightarrow\sqrt{x}-5< 0\left(\sqrt{x}+5>0\right)\\ \Leftrightarrow0\le x< 25\)
Bài 4:
\(a,A=\dfrac{16+2\cdot4+5}{4-3}=29\\ b,B=\dfrac{2\sqrt{x}-9-x+9+2x-3\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ B=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\\ c,P=\dfrac{x+2\sqrt{x}+5}{\sqrt{x}-3}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}=\dfrac{x+2\sqrt{x}+5}{\sqrt{x}+1}\\ P=\dfrac{\left(\sqrt{x}+1\right)^2+4}{\sqrt{x}+1}=\sqrt{x}+1+\dfrac{4}{\sqrt{x}+1}\\ P\ge2\sqrt{\left(\sqrt{x}+1\right)\cdot\dfrac{4}{\sqrt{x}+1}}=2\sqrt{4}=4\\ P_{min}=4\Leftrightarrow\left(\sqrt{x}+1\right)^2=4\Leftrightarrow\sqrt{x}+1=2\Leftrightarrow x=1\left(tm\right)\)

TL:
Tìm 1 cạnh của hình vuông: 280 : 4 = 70 ( ................ mik ko biết đơn vị là gì hết bạn ơi ! )
Diện tích hình vuông đó là: 70 x 70 = 4900 ( ..........2 )
Đáp số: 4900 .....2
Chúc bạn học tốt!
k mik nha!

1.A
2.A
3.B
4.C
5.B
6.C
7.A
8.A
9.B
10.A
11.B
12.A
13.C
14.B
15.B
16.A
17.A
18.A
19.A
20.C

\(\left(x+2\right)\left(\dfrac{360}{x}-6\right)=360\)
\(ĐK:x\ne0\)
\(\Leftrightarrow\left(x+2\right)\left(\dfrac{360-6x}{x}\right)=360\)
\(\Leftrightarrow360-6x+\dfrac{720-12x}{x}=360\)
\(\Leftrightarrow360x-6x^2+720-12x=360x\)
\(\Leftrightarrow6x^2+12x-720=0\)
\(\Delta=12^2-4.6.\left(-720\right)\)
\(=17424>0\)
`->` pt có 2 nghiệm
\(\left\{{}\begin{matrix}x_1=\dfrac{-12-\sqrt{17424}}{12}=-12\\x_2=\dfrac{-12+\sqrt{17424}}{12}=10\end{matrix}\right.\) ( tm )
Vậy \(S=\left\{-12;10\right\}\)
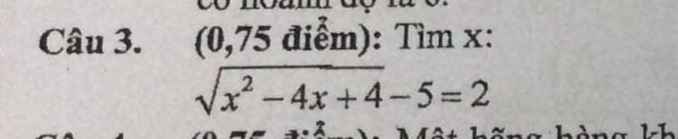

 giúp mình với, mk cần gấp ạ, cảm ơn mn rất nhìu !
giúp mình với, mk cần gấp ạ, cảm ơn mn rất nhìu ! ai giúp mình phần 1 với ạ
ai giúp mình phần 1 với ạ 









Bài 8:
a: Quy luật là số sau bằng số trước cộng thêm 5 đơn vị
b: A={3;5;8;13;18;23;28;33}
Bài 9:
a: Quy luật là số sau bằng số trước cộng thêm 3 đơn vị
b: B={2;5;8;11;14;17;20;23;26;29}
Bài 7:
a: A={6;7;8;9;11}
A={\(x\in\)N|5<x<12}
B={2;3;4;...;11}
B={\(x\in\)N|1<x<12}
b: C={6;7;8;9;11}