Cần gấp bài này ạ. Mình cảm ơn!!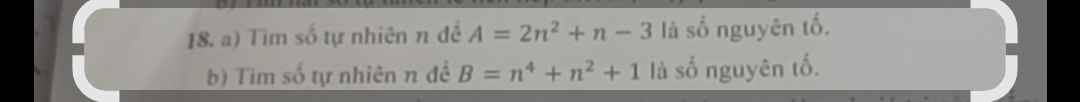
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





\(x=\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\)
\(\Rightarrow x^3=9+4\sqrt{5}+9-4\sqrt{5}+3\sqrt[3]{\left(9+4\sqrt[]{5}\right)\left(9-4\sqrt{5}\right)}\left(\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\right)\)
\(=18+3\sqrt{81-80}.x=18+3x\)\(\Rightarrow x^3-3x=18\left(1\right)\)
\(y=\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\)
\(\Rightarrow y^3=3+2\sqrt{2}+3-2\sqrt{2}+3\sqrt[3]{\left(3+2\sqrt{2}\right)\left(3-2\sqrt{2}\right)}\left(\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\right)\)
\(=6+3\sqrt[3]{9-8}.y=6+3y\)\(\Rightarrow y^3-3y=6\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow P=x^3+y^3-3\left(x+y\right)+1996=x^3-3x+y^3-3y+1996\)
\(=18+6+1996=2020\)

2:
a: =(1+căn 3)^2-5
=4+2căn 3-5
=2căn 3-1
b: \(=\sqrt{\dfrac{125}{7}\cdot\dfrac{35}{81}}=\sqrt{\dfrac{625}{81}}=\dfrac{25}{9}\)
c: \(=\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)-\sqrt{6}+\sqrt{2}\)
=2-căn 6+căn 2
3:
a: \(=\dfrac{2\sqrt{3}+3\sqrt{3}-\sqrt{3}}{\sqrt{3}}=2+3-1=5\)
b: \(=\dfrac{6\sqrt{2}+7\sqrt{2}-5\sqrt{2}}{\sqrt{2}}=13-5=8\)
c: \(=\dfrac{12-10+8}{2}=5\)
d: \(=\sqrt{\dfrac{1}{5}:5}-\sqrt{\dfrac{9}{5}:5}+\sqrt{5:5}\)
=1/5-3/5+1
=3/5


a: Ta có: BC⊥BA tại B
nên BC là tiếp tuyến của (A;AB)
b: Xét (A) có
CB là tiếp tuyến
CD là tiếp tuyến
Do đó: CB=CD
hay C nằm trên đường trung trực của BD(1)
Ta có: AB=AD
nên A nằm trên đường trung trực của BD(2)
Từ (1) và (2) suy ra AC là đường trung trực của BD
hay AC\(\perp\)BD
Giúp mình luôn câu c d được không:((( sắp hết h rồi mà không bt làm

a: Tỉ số là 3/2
b: Tỉ số phần trăm là;
40/(30+40+20+20+5)=34,78%







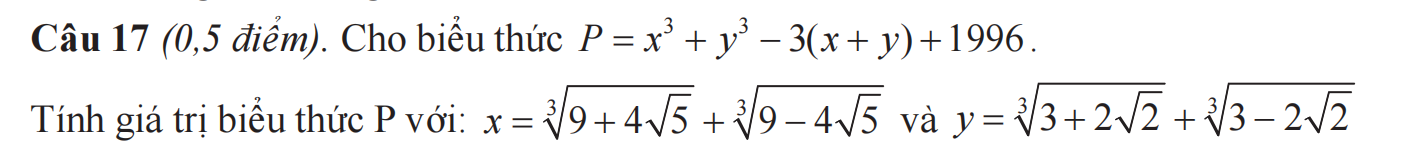 cảm ơn
cảm ơn 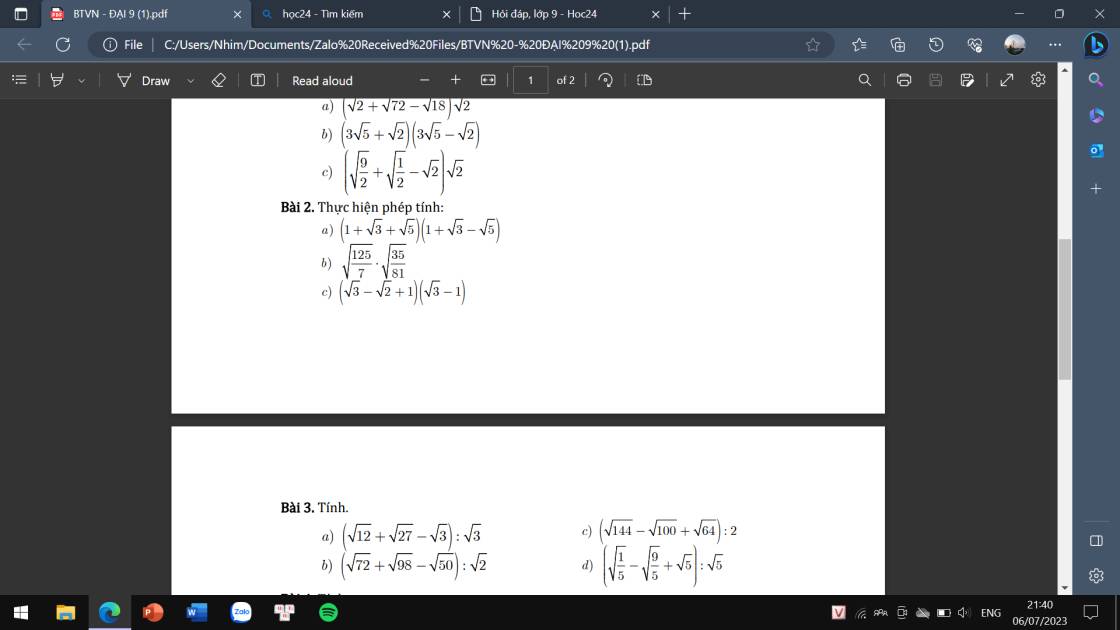





a: \(A=2n^2+n-3\)
\(=2n^2+3n-2n-3\)
\(=n\left(2n+3\right)-\left(2n+3\right)=\left(2n+3\right)\left(n-1\right)\)
Nếu n=0 thì \(A=\left(2\cdot0+3\right)\left(0-1\right)=-3< 0\)
=>Loại
Nếu n=1 thì \(A=\left(2\cdot1+3\right)\left(1-1\right)=0\)
=>Loại
Nếu n=2 thì \(A=\left(2\cdot2+3\right)\left(2-1\right)=7\) là số nguyên tố
=>Nhận
Khi n>2 thì \(A=\left(2n+3\right)\left(n-1\right)\) là tích của 2 số tự nhiên lớn hơn 1
=>A không phải là số nguyên tố
=>Loại
b: \(B=n^4+n^2+1=n^4+2n^2+1-n^2\)
\(=\left(n^2+1\right)^2-n^2=\left(n^2-n+1\right)\left(n^2+n+1\right)\)
Khi n=0 thì \(B=\left(0^2-0+1\right)\left(0^2+0+1\right)=1\)
=>Loại
Khi n=1 thì \(B=\left(1^2-1+1\right)\left(1^2+1+1\right)=3\) là số nguyên tố
=>Nhận
Khi n>1 thì \(B=\left(n^2-n+1\right)\left(n^2+n+1\right)\) là tích của hai số tự nhiên lớn hơn 1
=>Loại