tìm khoảng biến thiên của hàm số f(x) = \(\sqrt{2x-x^{2^{ }}}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-6}{2\cdot4}=\dfrac{-6}{8}=\dfrac{-3}{4}\\y=-\dfrac{6^2-4\cdot4\cdot\left(-5\right)}{4\cdot4}=-\dfrac{29}{4}\end{matrix}\right.\)
Bảng biến thiên là:
| x | -\(\infty\) -3/4 +\(\infty\) |
| y | -\(\infty\) -29/4 +\(\infty\) |

b: Hàm số đồng biến khi x>-3/4; nghịch biến khi x<-3/4
GTNN của hàm số là y=-29/4 khi x=-3/4

a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-10}{2\cdot\left(-3\right)}=\dfrac{10}{6}=\dfrac{5}{3}\\y=-\dfrac{10^2-4\cdot\left(-3\right)\cdot\left(-4\right)}{4\cdot\left(-3\right)}=\dfrac{13}{3}\end{matrix}\right.\)
Bảng biến thiên:
| x | -\(\infty\) 5/3 +\(\infty\) |
| y | +\(\infty\) 13/3 -\(\infty\) |

b: Hàm số đồng biến khi x<5/3; nghịch biến khi x>5/3
Giá trị nhỏ nhất là y=13/3 khi x=5/3


a. Với $x_1, x_2\in\mathbb{R}$ thỏa $x_1\neq x_2$ thì:
\(A=\frac{f(x_1)-f(x_2)}{x_1-x_2}=\frac{-2(x_1^2-x_2^2)+(x_1-x_2)}{x_1-x_2}=1-2(x_1+x_2)\)
Với $x_1,x_2> \frac{1}{4}$ thì $A< 0$ nên hàm số nghịch biến trên $(\frac{1}{4}; +\infty)$
Với $x_1,x_2< \frac{1}{4}$ thì $A>0$ nên hàm số đồng biến trên $(-\infty; \frac{1}{4})$
b. TXĐ: $D=(-\infty; 2]$
\(A=\frac{f(x_1)-f(x_2)}{x_1-x_2}=\frac{\sqrt{2-x_1}-\sqrt{2-x_2}}{x_1-x_2}=\frac{-1}{\sqrt{2-x_1}+\sqrt{2-x_2}}< 0\)
Vậy hàm số nghịch biến trên tập xác định $(-\infty;2]$
c. TXĐ: $D=[0;2]$
\(A=\frac{f(x_1)-f(x_2)}{x_1-x_2}=\frac{\sqrt{2x_1-x_1^2}-\sqrt{2x_2-x_2^2}}{x_1-x_2}=\frac{2-(x_1+x_2)}{\sqrt{2x_1-x_1^2}+\sqrt{2x_2-x_2^2}}\)
Nếu $x_1,x_2\in (1;2)$ thì $A<0$ nên hàm số nghịch biến trên $(1;2)$
Nếu $x_1,x_2\in (0;1)$ thì $A>0$ nên hàm số nghịch biến trên $(0;1)$


Ta có ![]()
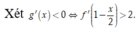
= TH1: ![]() Do đó hàm số nghịch biến trên (-4;-2)
Do đó hàm số nghịch biến trên (-4;-2)
= TH2: ![]() nên hàm số chỉ nghịch biến trên khoảng (2-2a;4) chứ không nghịch biến trên toàn khoảng (2;4)
nên hàm số chỉ nghịch biến trên khoảng (2-2a;4) chứ không nghịch biến trên toàn khoảng (2;4)
Vậy hàm số 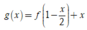 nghịch biến trên (-4;-2)
nghịch biến trên (-4;-2)
Chọn A.
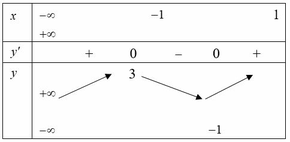

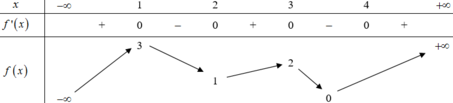

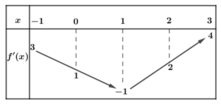
\(D=\left[0;2\right]\)
Có \(f'\left(x\right)=\dfrac{-x+1}{\sqrt{2x-x^2}},\forall x\in\left(0;2\right)\)
\(f'\left(x\right)=0\Leftrightarrow x=1\)
Vậy hàm số đã cho đồng biến trên \(\left(0;1\right)\) và nghịch biến trên \(\left(1;2\right)\)
ĐKXĐ: \(2x-x^2>=0\)
=>\(x^2-2x< =0\)
=>x(x-2)<=0
=>0<=x<=2
\(y=\sqrt{2x-x^2}\)
=>\(y'=\dfrac{\left(2x-x^2\right)'}{2\sqrt{2x-x^2}}=\dfrac{-2x+2}{2\sqrt{2x-x^2}}=\dfrac{-x+1}{\sqrt{2x-x^2}}\)
Đặt y'>0
=>-x+1>0
=>-x>-1
=>x<1
=>0<=x<1
=>Hàm số đồng biến khi 0<=x<1
Đặt y'<0
=>-x+1<0
=>-x<-1
=>x>1
=>1<x<=2
=>Hàm số nghịch biến khi 1<x<=2