 giải giúp e bài này với ạ, e đang cần gấp
giải giúp e bài này với ạ, e đang cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔHAC vuông tại H và ΔABC vuông tại A có
\(\widehat{C}\) chung
Do đó: ΔHAC~ΔABC
b: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=15^2+20^2=625\)
=>BC=25
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}BH\cdot BC=BA^2\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH\cdot25=15^2=225\\AH\cdot25=15\cdot20=300\end{matrix}\right.\)
=>BH=9; AH=12







\(a,ĐK:...\\ PT\Leftrightarrow x^2-6x=x^2-7x+10\\ \Leftrightarrow x=10\left(tm\right)\\ b,ĐK:...\\ PT\Leftrightarrow2x\left(4-x\right)-\left(2-2x\right)\left(8-x\right)=\left(8-x\right)\left(4-x\right)\\ \Leftrightarrow8x-2x^2+16+18x-2x^2=32-12x+x^2\\ \Leftrightarrow3x^2-38x+16=0\left(casio\right)\\ c,ĐK:...\\ PT\Leftrightarrow2x\left(x-4\right)-4x=0\\ \Leftrightarrow2x^2-12x=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=6\left(tm\right)\end{matrix}\right.\)



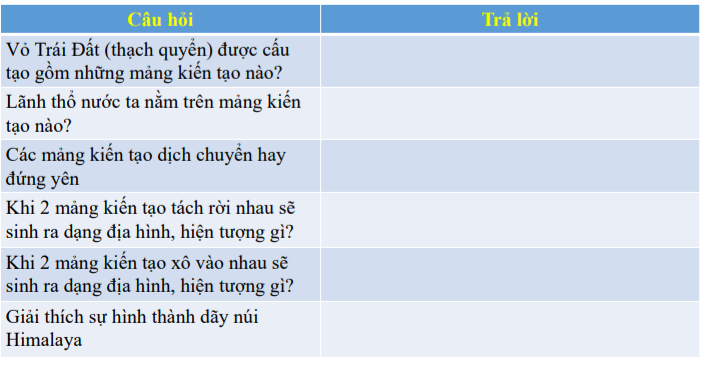 Mn giúp e bài này với ạ.E đang cần gấp ạ.
Mn giúp e bài này với ạ.E đang cần gấp ạ.




a: ΔOBC cân tại O
mà OI là đường trung tuyến
nên OI\(\perp\)BC
Xét tứ giác OASI có \(\widehat{OAS}+\widehat{OIS}=90^0+90^0=180^0\)
nên OASI là tứ giác nội tiếp
b: ΔOAD cân tại O
mà OS là đường cao
nên OS là phân giác của góc AOD
Xét ΔOAS và ΔODS có
OA=OD
\(\widehat{AOS}=\widehat{DOS}\)
OS chung
Do đó: ΔOAS=ΔODS
=>\(\widehat{OAS}=\widehat{ODS}\)
=>\(\widehat{ODS}=90^0\)
=>SD là tiếp tuyến của (O)