giúp e vớiii
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 1 2024
a: \(\dfrac{-2}{x^2+6x}=\dfrac{-2}{x\left(x+6\right)}\)
\(\dfrac{x}{x+6}=\dfrac{x\cdot x}{x\left(x+6\right)}=\dfrac{x^2}{x\left(x+6\right)}\)
b: \(\dfrac{11}{25-x^2}=\dfrac{-11}{x^2-25}=\dfrac{-11}{\left(x-5\right)\left(x+5\right)}=\dfrac{-11\left(x-5\right)}{\left(x-5\right)^2\cdot\left(x+5\right)}\)
\(\dfrac{2}{x^2-10x+25}=\dfrac{2}{\left(x-5\right)^2}=\dfrac{2\left(x+5\right)}{\left(x+5\right)\cdot\left(x-5\right)^2}\)
17 tháng 2 2022
Bài 2:
Xét ΔBDC có BE/ED=BF/FC
nên EF//DC
mà DC//AB
nên EF//AB
LN
2
YN
17 tháng 5 2023
x�x 652,36 + 298 x x�- 945,24 x x�= 128
x�x (652,36 + 298 – 945,24) = 128
x�x 5,12 = 128
x� = 128 : 5,12
x� = 25
LT
0
15 tháng 12 2021
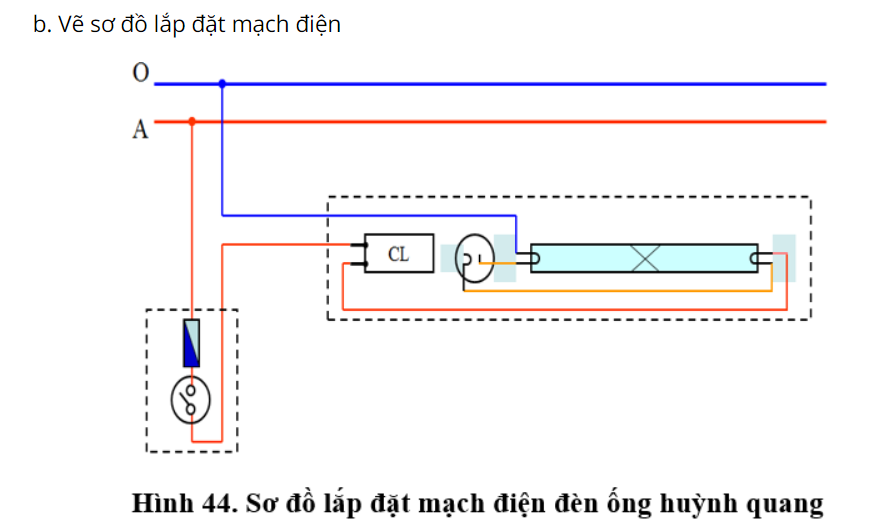
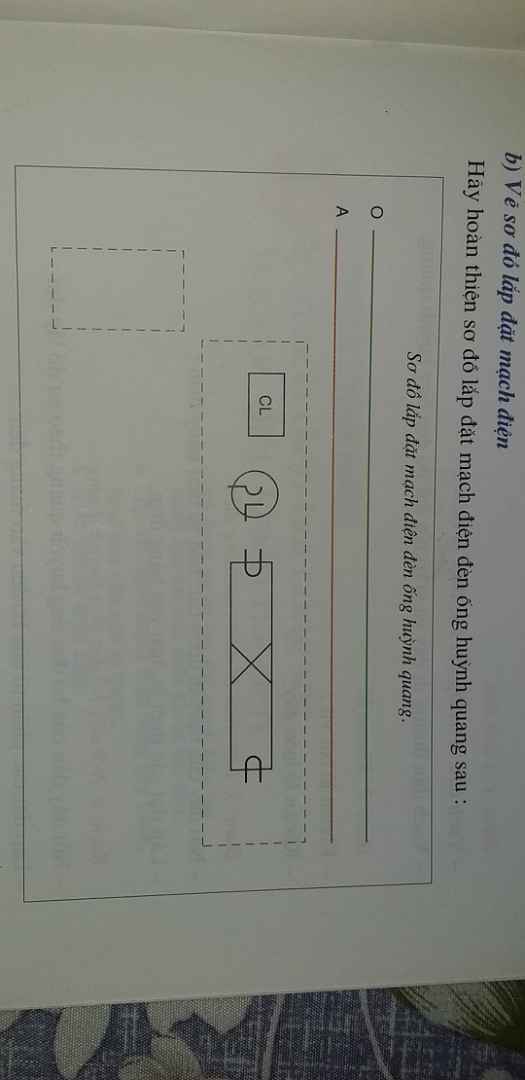
Nguồn: https://vietjack.com/giai-bai-tap-cong-nghe-9/ly-thuyet-thuc-hanh-lap-mach-dien-den-ong-huynh-quang.jsp
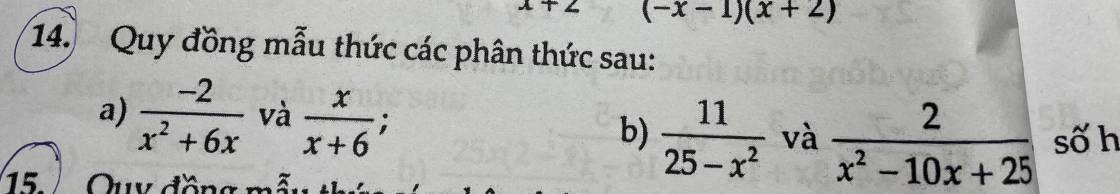
ĐKXĐ: \(\left\{{}\begin{matrix}x\ne0\\y\ne0\end{matrix}\right.\)
\(\left\{{}\begin{matrix}\dfrac{2}{3x}+\dfrac{4}{5y}=7\\\dfrac{3}{4x}-\dfrac{2}{5y}=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{2}{3x}+\dfrac{4}{5y}=7\\\dfrac{6}{4x}-\dfrac{4}{5y}=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{3x}+\dfrac{6}{4x}=7+6\\\dfrac{2}{3x}+\dfrac{4}{5y}=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{2}{3x}+\dfrac{3}{2x}=13\\\dfrac{2}{3x}+\dfrac{4}{5y}=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{x}\left(\dfrac{2}{3}+\dfrac{3}{2}\right)=13\\\dfrac{2}{3x}+\dfrac{4}{5y}=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}\cdot\dfrac{13}{6}=13\\\dfrac{2}{3x}+\dfrac{4}{5y}=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{x}=13:\dfrac{13}{6}=6\\\dfrac{2}{3x}+\dfrac{4}{5y}=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{6}\\\dfrac{4}{5y}=7-\dfrac{2}{3x}=7-\dfrac{2}{3\cdot\dfrac{1}{6}}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{1}{6}\\\dfrac{4}{5y}=7-\dfrac{2}{\dfrac{1}{2}}=7-2\cdot2=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{1}{6}\\5y=\dfrac{4}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{6}\\y=\dfrac{4}{15}\end{matrix}\right.\left(nhận\right)\)