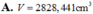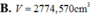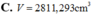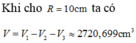Một vật hình cầu, bán kính \(R\). Cho mật độ khối lượng của vật phụ thuộc vào khoảng cách \(r\) đến tâm của nó theo quy luật \(\rho=\dfrac{3m}{7\pi R^3}\left(1 \dfrac{r}{R}\right)\), với \(m\) là hằng...

TM

Tô Mì

19 tháng 5

Một vật hình cầu, bán kính \(R\). Cho mật độ khối lượng của vật phụ thuộc vào khoảng cách \(r\) đến tâm của nó theo quy luật \(\rho=\dfrac{3m}{7\pi R^3}\left(1+\dfrac{r}{R}\right)\), với \(m\) là hằng số dương. Tìm khối lượng và momen quán tính của vật đối với trục quay qua tâm của...

Đọc tiếp

#Vật lý lớp 11

0

QT

Quoc Tran Anh Le

Giáo viên

5 tháng 9 2023

Khối lượng riêng của thép là \(7850kg\)/m³. Tính khối lượng của một quả cầu thép bán kính 0,15 m. Cho biết công thức tính thể tích của khối cầu là \(V=\dfrac{4}{3}\pi r^3\), với r là bán kính quả cầu.

#Vật lý lớp 10

1

HQ

Hà Quang Minh

Giáo viên

3 tháng 11 2023

Thể tích của quả cầu thép là:

\(V = \frac{4}{3}\pi {r^3} = \frac{4}{3}\pi .0,{15^3} = 0,014\left( {{m^3}} \right)\)

Khối lượng của quả cầu thép là:

\(m = \rho V = 7850.0,014 = 110\left( {kg} \right)\)

Đúng(0)

HN

Hùng Nguyễn

19 tháng 8 2021

Một khối cầu đặc đồng chất, tâm O, bán kính R, khối lượng m, bị khoét một lỗ hổng cũng có dạng hình cầu tâm O’ bán kính R/2, như hình 3.34. Mômen quán tính của phần còn lại của khối cầu đối với trục Oy (tính theo m, R) là bao nhiêu ?

#Vật lý lớp 12

0

HD

Hoàng Đức Long

24 tháng 10 2017

Trong một quả cầu bằng chì bán kính R, người ta khoét một lỗ hình cầu bán kính R/2Tìm lực do quả cầu tác dụng lên vật nhỏ m trên đường nối tâm hai hình cầu, cách tâm hình cầu lớn một đoạn d, biết rằng khi chưa khoét quả cầu có khối lượng M. A. F = G M n 7 d 2 - 8 d R + 2 R 2 8 d 2 d - R ...

Đọc tiếp

#Vật lý lớp 10

1

VT

Vũ Thành Nam

24 tháng 10 2017

Chọn A.

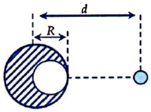
Phần khoét đi, nếu đặt lại chỗ cũ sẽ hút m lực hấp dẫn:

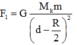
Lực hấp dẫn do cả quả cầu đặc tác dụng lên m:

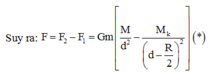
Do quả cầu đồng chất nên:

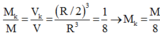
Thay vào (*) rồi biến đổi ta được

Đúng(0)

S

Sakura

16 tháng 5 2021 - olm

Cho hình trụ ABCD nội tiếp khối cầu tâm O bán kính R, biết AB=R. Thể tích của khối cầu nằm ngoài khối trụ là:A. \(\frac{\pi R^3}{6}\left(4-3\sqrt{3}\right)\) B.\(\frac{\pi R^3}{12}\left(16-3\sqrt{3}\right)\) C. \(\frac{\pi R^3}{12}\left(8-3\sqrt{3}\right)\) D.\(\frac{\pi R^3}{3}\left(8-3\sqrt{3}\right)\)( Có lời giải...

Đọc tiếp

#Toán lớp 9

2

T

🤣🤣🤣 Ŧùɔ

16 tháng 5 2021

V(tru) =π.R^2/4.R√3
V(cau)=4/3.π.R^3
Vnktru=πR^3(4/3-√3/4)
=πR^3/12.(16-3√3)
Chọn (B).

Đúng(0)

T

🤣🤣🤣 Ŧùɔ

16 tháng 5 2021

Vtru =π.R^2/4.R√3

Vcau=4/3.π.R^3

Vnktru=πR^3(4/3-√3/4)

=πR^3/12.(16-3√3)

Chọn (B).

Đúng(0)

B

Buddy

17 tháng 1 2023

Khối lượng riêng của thép là 7850kg/m³. Tính khối lượng của một quả cầu thép bán kính 0,15 m. Cho biết công thức tính thể tích của khối cầu là V=\(\dfrac{4}{3}\)πr³, với r là bán kính quả cầu.

#Vật lý lớp 10

1

AM

Ami Mizuno

17 tháng 1 2023

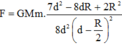
Thể tích của quả cầu thép là: \(V=\dfrac{4}{3}\pi r^3=\dfrac{4}{3}\pi.\left(0,15\right)^3=0,0045\pi\left(m^3\right)\)

Khối lượng của quả cầu thép là: \(m=DV=7850.0,0045\pi\approx111\left(kg\right)\)

Đúng(1)

B

Bướm

18 tháng 12 2020

một viên bi nhỏ có khối lượng m bằng 100 gam bán kính r = 2 cm được treo vào điểm cố định a nhỏ dây AB dài 20 cm và nằm trên mặt cầu tâm O có bán kính r = 8 cm khoảng cách từ a đến mặt cầu là AC 15 cm lấy g bằng 10 m trên giây bình tìm lực căng của dây và lực do có cầu ném lên mặt cầu

#Vật lý lớp 10

1

HT

Hoàng Tử Hà

19 tháng 12 2020

Có hình ko bạn? Đề bài ko có dấu chấm dấu phẩy nên đọc ko hiểu gì :v

Đúng(0)

TN

Tuấn Nguyễn

20 tháng 2 2023

Một hình nón có bán kính đáy là R,diện tích xung quanh bằng hai lần diện tích đáy của nó.Khi đó thể tích hình nón bằngA.\(\dfrac{\pi R^3\sqrt{3}}{3}\)cm3 B.\(\pi R^3\sqrt{3}\)cm3 C.\(\dfrac{\pi R^3\sqrt{5}}{3}\)cm3 D.\(\dfrac{\pi...

Đọc tiếp

#Toán lớp 9

2

NL

Nguyễn Lê Phước Thịnh

20 tháng 2 2023

Chọn C

Đúng(1)

DV

ĐỖ VÂN KHÁNH

20 tháng 2 2023

chọn C

Đúng(1)

PT

Pham Trong Bach

14 tháng 8 2017

Cho khối cầu tâm O và bán kính R. Xét hai mặt phẳng (P), (Q) thay đổi song song với nhau có khoảng cách là R và cùng cắt khối cầu theo tiết diện là hai hình tròn. Tổng diện tích của hai hình tròn này có giá trị lớn nhất là A. 5 4 πR 2 B. πR 2 C. 7 4 πR 2 D. 3 2 πR 2 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

14 tháng 8 2017

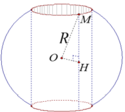
HD: Gọi x, y lần lượt là khoảng cách từ tâm mặt cầu đến các đường tròn thiết diện

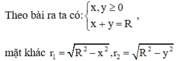
Tổng diện tích của hai hình tròn này là:

Đúng(0)

B

Buddy

17 tháng 7 2023

Lực hấp dẫn do Trái Đất tác dụng lên một đơn vị khối lượng ở khoảng cách \(r\) ở tỉnh từ tâm của nó là\(F\left( r \right) = \left\{ {\begin{array}{*{20}{c}}{\frac{{GM{\rm{r}}}}{{{R^3}}}}&{khi\,\,0 < x < R}\\{\frac{{GM}}{{{r^2}}}}&{khi\,\,r \ge R}\end{array}} \right.\)trong đó \(M\) là khối lượng, \(R\) là bán kính của Trái Đất, \(G\) là hằng số hấp dẫn.Hàm số \(F\left( r \right)\) có liên tục trên \(\left( {0; + \infty } \right)\)...

Đọc tiếp

#Toán lớp 11

1

HQ

Hà Quang Minh

Giáo viên

22 tháng 9 2023

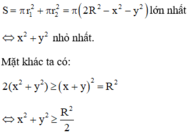
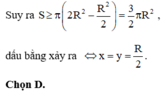
Hàm số \(F\left( r \right)\) có tập xác định là \(\left( {0; + \infty } \right)\).

Hàm số \(F\left( r \right)\) xác định trên từng khoảng \(\left( {0;R} \right)\) và \(\left( {R; + \infty } \right)\) nên hàm số liên tục trên các khoảng đó.

Ta có: \(F\left( R \right) = \frac{{GM}}{{{R^2}}}\)

\(\begin{array}{l}\mathop {\lim }\limits_{r \to {R^ + }} F\left( r \right) = \mathop {\lim }\limits_{r \to {R^ + }} \frac{{GM}}{{{r^2}}} = \frac{{GM}}{{{R^2}}}\\\mathop {\lim }\limits_{r \to {R^ - }} F\left( r \right) = \mathop {\lim }\limits_{r \to {R^ - }} \frac{{GMr}}{{{R^3}}} = \frac{{GMR}}{{{R^3}}} = \frac{{GM}}{{{R^2}}}\end{array}\)

Vì \(\mathop {\lim }\limits_{r \to {R^ + }} F\left( r \right) = \mathop {\lim }\limits_{r \to {R^ - }} F\left( r \right) = \frac{{GM}}{R}\) nên \(\mathop {\lim }\limits_{r \to R} F\left( r \right) = \frac{{GM}}{R} = F\left( R \right)\).

Vậy hàm số \(F\left( r \right)\) liên tục tại điểm \({r_0} = R\).

Vậy hàm số \(F\left( r \right)\) liên tục trên \(\left( {0; + \infty } \right)\).

Đúng(0)

PT

Pham Trong Bach

7 tháng 1 2019

Có một khối cầu bằng gỗ bán kính R=10cm. Sau khi cưa bằng hai chỏm cầu có bán kính đáy bằng một nửa R đối xứng nhau qua tâm khối cầu, một người thợ khoan xuyên tâm khối cầu. Người thợ đã khoan bỏ đi phần hình trụ có trục của nó trùng với trục hình cầu; mặt cắt của hình trụ vuông góc với trục hình trụ là một hình tròn có bán kính bằng 1/2R. Tính thể tích V của phần còn lại...

Đọc tiếp