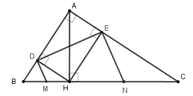
Cho tam giác ABC vuông tại A . AH vuông góc vói BC . Vẽ HD vuông góc với AB (D thuộc AB) , Vẽ HE vuông góc với AC (E thuộc AC). Biết BH = 9cm , CH=16cm . Tính DE ??
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 1 2023
a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC và AH là phân giác của góc BAC
=>góc BAH=góc CAH
b: \(BH=\sqrt{5^2-4^2}=3\left(cm\right)\)
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
góc DAH=góc EAH
Do đó: ΔADH=ΔAEH
=>AD=AE
=>ΔADE cân tại A
11 tháng 10 2023
a: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC=\sqrt{9^2+12^2}=15\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\BH\cdot BC=AB^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=\dfrac{9\cdot12}{15}=7.2\left(cm\right)\\BH=\dfrac{9^2}{15}=5.4\left(cm\right)\end{matrix}\right.\)
b:
ΔAHB vuông tại H có HD là đường cao
nên \(HD\cdot AB=HA\cdot HB\)
ΔAHC vuông tại H có HE là đường cao
nên \(HE\cdot AC=HA\cdot HC\)
\(HD\cdot AB+HE\cdot AC\)
\(=HA\cdot HB+HA\cdot HC=HA\cdot\left(HB+HC\right)\)
\(=HA\cdot BC=AB\cdot AC\)
c: Xét tứ giác ADHE có \(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
=>ADHE là hình chữ nhật
ΔABC vuông tại A có AM là trung tuyến
nên AM=MB=MC
\(\widehat{IEA}+\widehat{IAE}=\widehat{DEA}+\widehat{IAC}\)
\(=\widehat{DHA}+\widehat{MCA}\)
\(=\widehat{ABC}+\widehat{ACB}=90^0\)
=>AM vuông góc DE tại I
ΔADE vuông tại A có AI là đường cao
nên \(\dfrac{1}{AI^2}=\dfrac{1}{AE^2}+\dfrac{1}{AD^2}\)
CM
24 tháng 6 2019
Tứ giác AEHD là hình chữ nhật vì: A ^ = E ^ = D ^ = 90 o nên DE = AH.
Xét ABC vuông tại A có: A H 2 = HB.HC = 9.16 = 144 => AH = 12
Nên DE = 12cm
Đáp án cần chọn là: A
27 tháng 6 2023
a: ΔABC cân tại A có AH là phân giác
nên H là trung điểm của BC
ΔABC cân tại A có AH là trung tuyến
nên AH vuông góc BC
b: BH=CH=12/2=6cm
AH=căn AB^2-AH^2=8cm
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
góc DAH=góc EAH
=>ΔADH=ΔAEH
=>AD=AE và HD=HE
=>ΔHDE cân tại H
d: Xét ΔABC có AD/AB=AE/AC
nên DE//BC
5 tháng 1 2021
a, xét tam giác ABH à tg ACH có AH chung
^BAH = ^CAH do AH là pg
AB = AC (gt)
=> tg ABH = tg ACH (c-g-c)
b, tg ABH = tg ACH (câu a )
=> ^AHC = ^AHB
mà ^AHC + ^AHB = 180
=> ^AHC = 90
=> AH _|_ BC
c, xét tam giác ADH và tam giác AEH có : AE chung
^ADH = ^AEH = 90
^bah = ^cah
=> Tg ADH= tg AEH (ch-gn)
=> AE = AD
=> tg AED cân tại A => ^ADE = (180 - ^BAC) : 2
tg ABC cân tại A => ^ABC = (180 - ^bac) : 2
=> ^ade = abc
mà ^ade đồng vị ^abc
=> de // bc