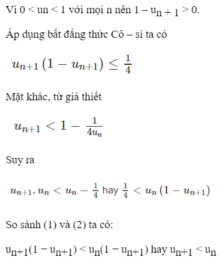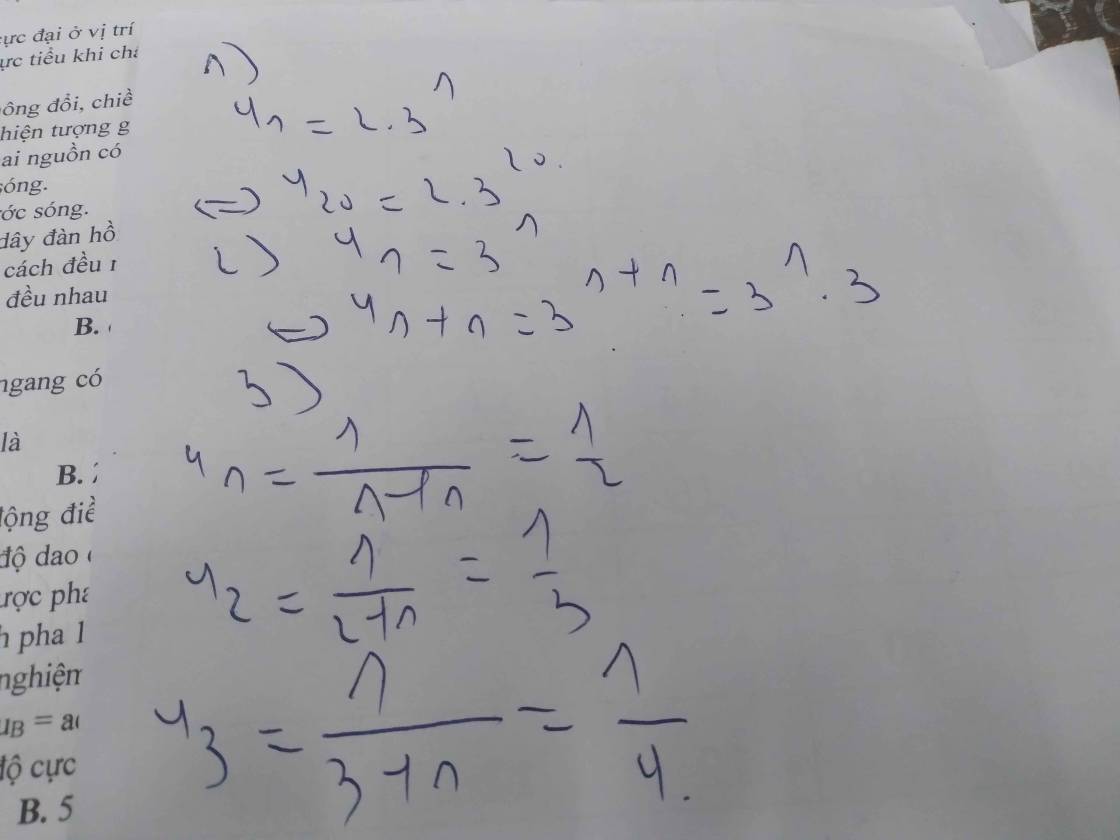Cho dãy : n+1;2n+3;3n+5;...
A_Viết số 100 trong dãy
B_tìm n sao cho tổng 100 số hạng đầu tiên bằng 60500
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
uses crt;
var a:array[1..1000000]of longint;
i,n,x:longint;
begin
clrscr;
write('Nhap n='); readln(n);
for i:=1 to n do
begin
write('A[',i,']='); readln(a[i]);
end;
write('Nhap x='); readln(x);
for i:=1 to n do
if a[i]<>x then write(a[i]:4);
readln;
end.

Câu 1: Cho dãy A là dãy giảm gồm N (N<=250) số
nguyên dương A1....AN và số nguyên K. Hãy tìm kiếm số
nguyên K trong dãy A.
A. Xác định bài toán
- B. Viết thuật toán tìm kiếm nhị phân|cho bài
toán. viết 2 cách
#include <bits/stdc++.h>
using namespace std;
long long i,n,x,k;
int main()
{
cin>>n>>k;
for (i=1; i<=n; i++)
{
cin>>x;
if (x==k) cout<<i<<" ";
}
return 0;
}

input: Dãy số nguyên
Output: Kiểm tra xem dãy có đối xứng không
*Thuật toán
Bước 1: Nhập n và nhập dãy số
Bước 2: i←1; kt←true;
Bước 3: Nếu a[i]<>a[n-i+1] thì kt←false;
Bước 4: i←i+1;
Bước 5: Nếu i<=n thì quay lại bước 3
Bước 6: Nếu kt=true thì đây là dãy đối xứng và ngược lại
Bước 7: Kết thúc

Chọn A
Trong bốn dãy số chỉ có yn=n/(n+1) < 1 nên có 1 dãy bị chặn trên

Dễ thấy \(u_n>0,\forall n\inℕ^∗\).
Ta có \(u_{n+1}-u_n=\dfrac{u_n^2+2021}{2u_n}-u_n=\dfrac{2021-u_n^2}{2u_n}\)
Với \(n\ge2\) thì \(u_n=\dfrac{u_{n-1}^2+2021}{2u_{n-1}}\) \(=\dfrac{u_{n-1}}{2}+\dfrac{2021}{2u_{n-1}}\) \(>2\sqrt{\dfrac{u_{n-1}}{2}.\dfrac{2021}{2u_{n-1}}}\) \(=\sqrt{2021}\)
Vậy \(u_n>\sqrt{2021},\forall n\ge2\), suy ra \(u_{n+1}-u_n=\dfrac{2021-u_n^2}{2u_n}< 0,\forall n\inℕ^∗\)
\(\Rightarrow\) Dãy \(\left(u_n\right)\) là dãy giảm. Mà \(u_n>\sqrt{2021}\) \(\Rightarrow\left(u_n\right)\) có giới hạn hữu hạn. Đặt \(\lim\limits_{n\rightarrow+\infty}u_n=L\) \(\Rightarrow L=\dfrac{L^2+2021}{2L}\) \(\Leftrightarrow L=\sqrt{2021}\)
Vậy \(\lim\limits_{n\rightarrow+\infty}u_n=\sqrt{2021}\)
Dễ thấy ��>0,∀�∈N∗un>0,∀n∈N∗.
Ta có ��+1−��=��2+20212��−��=2021−��22��un+1−un=2unun2+2021−un=2un2021−un2
Với �≥2n≥2 thì ��=��−12+20212��−1un=2un−1un−12+2021 =��−12+20212��−1=2un−1+2un−12021 >2��−12.20212��−1>22un−1.2un−12021 =2021=2021
Vậy ��>2021,∀�≥2un>2021,∀n≥2, suy ra ��+1−��=2021−��22��<0,∀�∈N∗un+1−un=2un2021−un2<0,∀n∈N∗
⇒⇒ Dãy (��)(un) là dãy giảm. Mà ��>2021un>2021 ⇒(��)⇒(un) có giới hạn hữu hạn. Đặt lim�→+∞��=�n→+∞limun=L ⇒�=�2+20212�⇒L=2LL2+2021 ⇔�=2021⇔L=2021
Vậy lim�→+∞��=2021n→+∞limun=2021