 giúp em vs ạ em cảm ơn nhiều
giúp em vs ạ em cảm ơn nhiều
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1) \(\sqrt{\dfrac{1}{200}}\) 2) \(\dfrac{5}{1-\sqrt{6}}\)
\(=\sqrt{\dfrac{1^2}{10^2.2}}\) \(=\dfrac{1-\sqrt{6}+4+\sqrt{6}}{1-\sqrt{6}}\)
\(=\dfrac{1}{10\sqrt{2}}\) \(=1+\dfrac{4+\sqrt{6}}{1-\sqrt{6}}\)
Bài 2:
1. \(\sqrt{2x-5}=7\) ĐKXĐ: \(x\ge\dfrac{5}{2}\)
<=> 2x - 5 = 72
<=> 2x - 5 = 49
<=> 2x = 54
<=> x = 27 (TM)
2. \(3+\sqrt{x-2}=4\) ĐKXĐ: \(x\ge2\)
<=> \(\sqrt{x-2}=1\)
<=> x - 2 = 1
<=> x = 3 (TM)
3. \(\sqrt{x^2-2x+1}=1\)
<=> \(\sqrt{\left(x-1\right)^2}=1\)
<=> \(|x-1|=1\)
<=> \(\left[{}\begin{matrix}x-1=1\\x-1=-1\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}x=2\\x=0\end{matrix}\right.\)
4. \(\sqrt{x^2-4x+4}=1\)
<=> \(\sqrt{\left(x-2\right)^2}=1\)
<=> \(|x-2|=1\)
<=> \(\left[{}\begin{matrix}x-2=1\\x-2=-1\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)
5. \(\sqrt{4x^2+1-4x}=\sqrt{x^2+16+8x}\)
<=> \(\left(\sqrt{4x^2+1-4x}\right)^2=\left(\sqrt{x^2+16+8x}\right)^2\)
<=> \(|4x^2+1-4x|=|x^2+16+8x|\)
<=> \(\left[{}\begin{matrix}4x^2+1-4x=x^2+16+8x\\4x^2+1-4x=-\left(x^2+16+8x\right)\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}4x^2-x^2-4x-8x+1-16=0\\4x^2+1-4x=-x^2-16-8x\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}3x^2-12x-15=0\\5x^2+4x+17=0\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}3x^2+3x-15x-15=0\\VNghiệm\end{matrix}\right.\)
<=> 3x(x + 1) - 15(x + 1) = 0
<=> (3x - 15)(x + 1) = 0
<=> \(\left[{}\begin{matrix}3x-15=0\\x+1=0\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)

1: \(\sqrt{\dfrac{1}{200}}=\dfrac{\sqrt{2}}{20}\)
2: \(\dfrac{5}{1-\sqrt{6}}=-1-\sqrt{6}\)
3: \(\dfrac{1}{1-\sqrt{2}}-\dfrac{1}{1+\sqrt{2}}\)
\(=\dfrac{1+\sqrt{2}-1+\sqrt{2}}{-1}\)
\(=-2\sqrt{2}\)

a: \(23AC1D_{16}=2337821_{10}\)
b: \(FC3DE_{16}=1033182_{10}\)

2: Ta có: \(\sqrt{16-6\sqrt{7}}\cdot\left(3+\sqrt{7}\right)\)
\(=\left(3-\sqrt{7}\right)\left(3+\sqrt{7}\right)\)
=9-7
=2
3: Ta có: \(\left(\sqrt{6}+\sqrt{14}\right)\cdot\sqrt{5-2\sqrt{21}}\)
\(=\left(\sqrt{7}+\sqrt{3}\right)\left(\sqrt{7}-\sqrt{3}\right)\)
=7-3
=4
\(1,=\sqrt{\left(5+2\sqrt{6}\right)^2}-\sqrt{\left(3-\sqrt{6}\right)^2}=5+2\sqrt{6}-3+\sqrt{6}=2+3\sqrt{6}\\ 2,=\sqrt{\left(3-\sqrt{7}\right)^2}\left(3+\sqrt{7}\right)=\left(3-\sqrt{7}\right)\left(3+\sqrt{7}\right)=9-7=2\\ 3,=\left(\sqrt{3}+\sqrt{7}\right)\sqrt{10-2\sqrt{21}}=\left(\sqrt{3}+\sqrt{7}\right)\sqrt{\left(\sqrt{7}-\sqrt{3}\right)^2}\\ =\left(\sqrt{7}+\sqrt{3}\right)\left(\sqrt{7}-\sqrt{3}\right)=7-3=4\\ 4,=\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{6+2\sqrt{5}}+\sqrt{4-2\sqrt{3}}\right)\\ =\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+1+\sqrt{3}-1\right)\\ =\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+\sqrt{3}\right)=5-3=2\)
\(5,\\ =\sqrt{\left(3\sqrt{3}-5\right)^2}+\sqrt{\left(5-2\sqrt{3}\right)^2}=3\sqrt{3}-5+5-2\sqrt{3}=\sqrt{3}\\ 6,=\sqrt{13-4\sqrt{10}}-\sqrt{53+12\sqrt{10}}\\ =\sqrt{\left(2\sqrt{2}-\sqrt{5}\right)^2}-\sqrt{\left(3\sqrt{5}-2\sqrt{2}\right)^2}\\ =2\sqrt{2}-\sqrt{5}-3\sqrt{5}+2\sqrt{2}=4\sqrt{2}-4\sqrt{5}\)




EX1:
1. A
2.A
3.A
4.D
5.D
6.A
7.C
8.B
9.B
10.C
11.B
EX2:
1. Tired
2. gives her
3. lot of
4.much does
5. as expensive as


h) \(=8-12y+6y^2-y^3\)
i) \(=8y^3-125\)
j) \(=27y^3+64\)
k) \(=x^3-9x^2+27x-27+8-12x+6x-x^3=-9x^2+21x-19\)



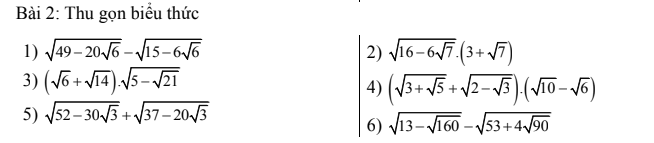






 Giúp em vs ạ em cảm ơn nhiều 😄😄😄😄
Giúp em vs ạ em cảm ơn nhiều 😄😄😄😄
a: Xét tứ giác AOBM có \(\widehat{OAM}+\widehat{OBM}=90^0+90^0=180^0\)
nên AOBM là tứ giác nội tiếp
b: Xét ΔAOM vuông tại A có \(sinAMO=\dfrac{AO}{OM}=\dfrac{1}{2}\)
nên \(\widehat{AMO}=30^0\)
Xét (O) có
MA,MB là các tiếp tuyến
DO đó: MA=MB và MO là phân giác của góc AMB
MO là phân giác của góc AMB
=>\(\widehat{AMB}=2\cdot\widehat{AMO}=60^0\)
AOBM nội tiếp
=>\(\widehat{AOB}+\widehat{AMB}=180^0\)
=>\(\widehat{AOB}=120^0\)
Độ dài đường tròn (O) là:
\(C=2\cdot5\cdot3,14=31,4\left(cm\right)\)
Diện tích hình quạt tròn ứng với cung nhỏ AB là:
\(S_{q\left(AB\right)}=\Omega\cdot5^2\cdot\dfrac{120}{360}=5^2\cdot\dfrac{3.14}{3}=\dfrac{157}{6}\left(cm^2\right)\)
c: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: OM là phân giác của góc AOB
=>\(\widehat{AOM}=\widehat{BOM}=\dfrac{120^0}{2}=60^0\)
Xét ΔOAC có OA=OC và \(\widehat{AOC}=60^0\)
nên ΔOAC đều
=>AC=OC=OA=R
Xét ΔOCB có OC=OB và \(\widehat{COB}=60^0\)
nên ΔOCB đều
=>OC=CB=OB=R
Xét tứ giác OACB có
OA=AC=CB=OB
nên OACB là hình thoi