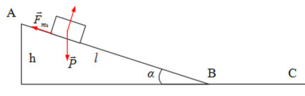
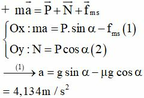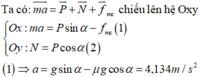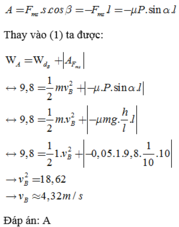Một vật có khối lượng m = 1kg trượt từ định mặt phẳng nghiên góc α = 30. Không vận tốc đầu ở độ cao 20 m. Do có ma sát khi đến chân mặt phẳng nghiêng góc vật đạt tốc độ 10 m/s. Lấy g = 10m/s2. Xác định hiệu suất của mặt phẳng nghiêng và hệ số ma sát trượt giữa vật và mặt phẳng nghiêng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Vận tốc vật chân mặt phẳng nghiêng:
\(mgh=\dfrac{1}{2}mv^2\) (Bảo toàn cơ năng)
\(\Rightarrow v=\sqrt{2gh}=\sqrt{2\cdot10\cdot0,45}=3\)m/s
b)Độ cao vật khi \(v'=2\)m/s:
\(mgh'=\dfrac{1}{2}mv'^2\)
\(\Rightarrow h'=\dfrac{1}{2g}\cdot v'^2=\dfrac{2^2}{2\cdot10}=0,2m\)
c)Vận tốc vật khi có độ cao \(z=0,3m\):
\(mgz=\dfrac{1}{2}mv''^2\)
\(\Rightarrow v''=\sqrt{2gz}=\sqrt{2\cdot10\cdot0,3}=\sqrt{6}\)m/s

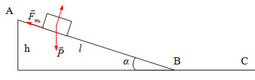
Ta có:
+ Cơ năng tại A:
\(W_A=mgh=1.9,8.1=9,8\left(J\right)\)
+ Trong khi vật chuyển động từ A đến B , tại B cơ năng chuyển hóa thành động năng tại B và công để thắng lực ma sát.
Áp dụng đl bảo toàn chuyển hóa năng lượng , ta có:
\(W_A=W_{db}-A_{Fms}\left(1\right)\)
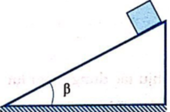
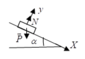
Chọn chiều dương trùng chiều chuyển động của vật , ta có:
+ Động năng tại B : \(W_{dg}=\dfrac{1}{2}mv^2_B\)
+ Công của lực ma sát:
\(A=F_{ms}.s.cos\beta=-F_{ms}.l=-\mu P.sin\alpha.l\)
Thay vào (1) ta được:
\(W_A=W_{dB}+\left|A_{Fms}\right|\)
\(\Leftrightarrow9,8=\dfrac{1}{2}mv^2_B+\left|-\mu.P.sin\alpha.l\right|\)
\(\Leftrightarrow9,8=\dfrac{1}{2}mv^2_B\left|-\mu mg.\dfrac{h}{l}.l\right|\)
\(\Leftrightarrow9,8=\dfrac{1}{2}1.v^2_B+\left|-0,05.1.9,8.\dfrac{1}{10}.10\right|\)
\(\Rightarrow v^2_B=18,62\)
\(\Rightarrow v_B\approx4,32m/s\)


![]()
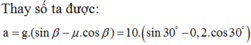
![]()
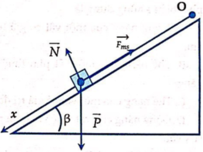
+ Theo công thức liên hệ a;v; S trong chuyển động thẳng biến đổi đều ta có:
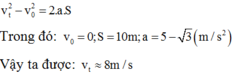

Áp dụng công thức về độ biến thiên động năng:
m v 2 /2 - m v 0 2 /2 = A = Fs
Với v 0 = 0 và F = Psin α - F m s = mg(sin α - μ cos α )
Từ đó suy ra:

Thay số, ta tìm được vận tốc của vật ở chân mặt phẳng nghiêng:
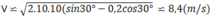

Ta có:
sin 30 = z s ⇒ z = s . sin 30 0 = 10. 1 2 = 5 ( m )
Chọn mốc thế năng tại chân dốc. Theo định luật bảo toàn cơ năng
W A = W B ⇒ m g z = 1 2 m v 2 ⇒ v = 2 g z ⇒ v = 2.10.5 = 10 ( m / s )

Chọn mặt đất làm gốc tính thế năng ( W t = 0), chiều chuyển động của vật trên mặt dốc là chiều dương. Do chịu tác dụng của lực ma sát (ngoại lực không phải là lực thế), nên cơ năng của vật không bảo toàn. Trong trường, hợp này, độ biến thiên cơ năng của vật có giá trị bằng công của lực ma sát:
W 2 - W 1 = (m v 2 /2 + mgz) - (m v 0 2 /2 + mg z 0 ) = A m s
Thay số: v 0 = 0, z 0 = 20 m, v = 15 m/s và z = 0, ta tìm được
A m s = m( v 2 /2 - g z 0 ) = 10( 15 2 /2 - 10.20) = -875(J)