cho tam giác abc vt a.đường cao AH, lấy K trên HC.qua K kẻ đt // với AB,cắt AH tại D.CM: AK vg CD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

KT
30 tháng 3 2018
a) Xét \(\Delta HBA\) và \(\Delta ABC\) có:
\(\widehat{AHB}=\widehat{CAB}=90^0\)
\(\widehat{ABC}\) CHỤNG
suy ra: \(\Delta HBA~\Delta ABC\)
b) Áp dụng định lý Pytago vào tam giác vuông ABC ta có:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow\)\(BC^2=12^2+16^2=400\)
\(\Leftrightarrow\)\(BC=\sqrt{400}=20\)cm
Áp dụng hệ thức lượng trong tam giác vuông ta có:
\(AH=\frac{AB.AC}{BC}=\frac{12.16}{20}=9,6\)
\(BH=\frac{AB^2}{BC}=\frac{12^2}{20}=7,2\)

21 tháng 6 2023
a: Xét ΔAHD vuông tại H và ΔAKD vuông tại K có
AH=AK
AD chung
=>ΔAHD=ΔAKD
b: AK=AH
DH=DK
=>AD là trung trực của HK
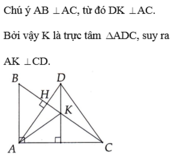
THAM KHẢO:
Ta có: AH là đường cao
=> CH vuông góc với AH
hay CH vuông góc với AD (1)
Ta có: DK // AB (gt)
=> DK vuông góc với AC (2) (AB vuông góc với AC, tam giác ABC vuông tại A)
Từ (1) và (2)
=> DK và CH là hai đường cao của tam giác ADC
Mà DK và CH cắt nhau tại K (K nằm trên HC)
=> K là trực tâm của tam giác ADC
Trong tam giác ADC có: AK cắt HC tại K
=> AK vuông góc CD (K là trực tâm của tam giác ADC) (đpcm)