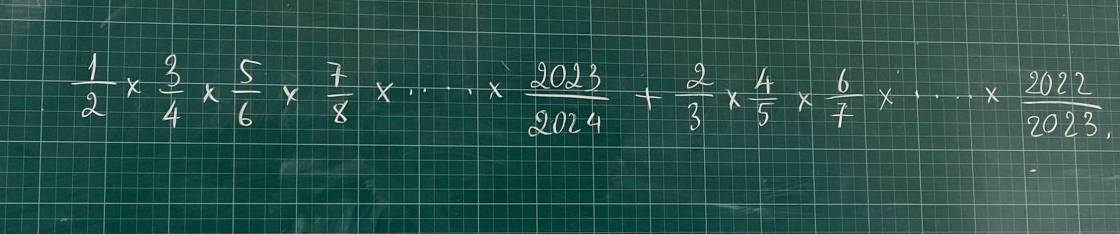Các thầy cô giúp e bài này với ạ, em cảm ơn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
DT
Đỗ Thanh Hải
CTVVIP
1 tháng 8 2021
1 inconvenience
2 voluntarily
3 industrial
4 break-taking
5 intentively
6 breakdown
7 preferable
8 economical
9 acceleration
10 misunderstanding
11 inhabitant
12 kidnapper
13 foggy
14 shouthern
15 decision
16 entertainment
17 information
18 pronounciation
TT
1
25 tháng 3 2023
1: vecto AC=(-1;-7)
=>VTPT là (-7;1)
PTTS là:
x=3-t và y=6-7t
Phương trình AC là:
-7(x-3)+1(y-6)=0
=>-7x+21+y-6=0
=>-7x+y+15=0
2: Tọa độ M là:
x=(3+2)/2=2,5 và y=(6-1)/2=2,5
PTTQ đường trung trực của AC là:
-7(x-2,5)+1(y-2,5)=0
=>-7x+17,5+y-2,5=0
=>-7x+y+15=0
3: \(AB=\sqrt{\left(-1-3\right)^2+\left(3-6\right)^2}=5\)
Phương trình (A) là:
(x-3)^2+(y-6)^2=AB^2=25
DT
Đỗ Thanh Hải
CTVVIP
2 tháng 8 2021
146 unemployed
147 communicative
148 disqualified
149 widen
150 completely
151 eaten
153 underpaid
154 misbehaved
155 resignation
156 widespread
157 imprisonment
158 underestimated
159 justify
160 single-minded
161 standardized
162 anxiety
163 growth
146 accustomed
NT
2
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 1
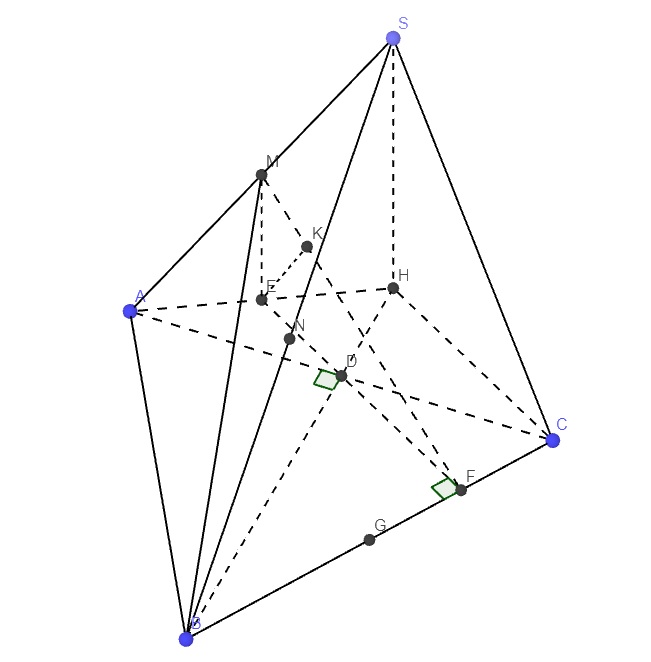
Gọi D là trung điểm AC
Trong mp (ABC), qua A kẻ đường thẳng vuông góc AB, qua C kẻ đường thẳng vuông góc AC, chúng cắt nhau tại H
Dễ dàng nhận ra hai tam giác vuông HAC và HAB có cặp cạnh huyền - cạnh góc vuông bằng nhau nên 2 tam giác bằng nhau
\(\Rightarrow HA=HC\Rightarrow H\) nằm trên trung trực AC (do AB=BC)
\(\Rightarrow H,A,D\) thẳng hàng
\(\left\{{}\begin{matrix}CH\perp BC\\SC\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SHC\right)\Rightarrow BC\perp SH\)
Tương tự ta có \(AB\perp\left(SHA\right)\Rightarrow AB\perp SH\)
\(\Rightarrow SH\perp\left(ABC\right)\)
Gọi E là trung điểm AH \(\Rightarrow ME\) là đường trung bình tam giác SAH
\(\Rightarrow ME||SH\Rightarrow ME\perp\left(ABC\right)\) đồng thời \(ME=\dfrac{1}{2}SH\)
Gọi G là trung điểm BC \(\Rightarrow AG\perp BC\), từ D kẻ \(DF\perp BC\Rightarrow DF||AG\Rightarrow DF\) là đường trung bình tam giác AGC
\(\Rightarrow DF=\dfrac{1}{2}AG=\dfrac{a\sqrt{3}}{4}\)
AGCH là hình thang (AG song song CH vì cùng vuông góc BC) \(\Rightarrow EF\) là đường trung bình hình thang
\(\Rightarrow EF\perp BC\Rightarrow E,D,F\) thẳng hàng
\(AH=\dfrac{AD}{cos\widehat{DAH}}=\dfrac{AD}{cos\widehat{ABD}}=\dfrac{AD}{cos30^0}=\dfrac{a\sqrt{3}}{3}\)
\(ED=\dfrac{1}{2}AH=\dfrac{a\sqrt{3}}{6}\) (trung tuyến tam giác vuông)
\(\Rightarrow EF=ED+DF=\dfrac{5a\sqrt{3}}{12}\)
Trong tam giác vuông MEF, từ E kẻ \(EK\perp MF\)
\(\left\{{}\begin{matrix}ME\perp\left(ABC\right)\Rightarrow ME\perp BC\\EF\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(MEF\right)\Rightarrow BC\perp EK\)
\(\Rightarrow EK\perp\left(MBC\right)\Rightarrow EK=d\left(E;\left(MBC\right)\right)\)
\(SB=2NB\Rightarrow d\left(S;\left(MBC\right)\right)=2d\left(N;\left(MBC\right)\right)\)
\(SM=AM\Rightarrow d\left(S;\left(MBC\right)\right)=d\left(A;\left(MBC\right)\right)\)
\(AC=2DC\Rightarrow d\left(A;\left(MBC\right)\right)=2d\left(D;\left(MBC\right)\right)\)
\(\dfrac{EF}{DF}=\dfrac{5}{3}\Rightarrow d\left(E;\left(MBC\right)\right)=\dfrac{5}{3}d\left(D;\left(MBC\right)\right)=\dfrac{5}{3}d\left(N;\left(MBC\right)\right)\)
\(\Rightarrow EK=\dfrac{5}{3}.\dfrac{3a}{7}=\dfrac{5a}{7}\)
\(\dfrac{1}{EK^2}=\dfrac{1}{ME^2}+\dfrac{1}{EF^2}\Rightarrow ME=\dfrac{EF.EK}{\sqrt{EF^2-EK^2}}=5a\)
\(\Rightarrow SH=2ME=10a\)
\(V=\dfrac{1}{3}.10a.\dfrac{a^2\sqrt{3}}{4}=\dfrac{5a^3\sqrt{3}}{6}\)
NT
6
HP
20 tháng 9 2021
3.
\(y=\dfrac{1-sin^24x}{5}=\dfrac{cos^24x}{5}\)
\(cos4x\in\left[-1;1\right]\Rightarrow cos^24x\in\left[0;1\right]\Rightarrow y\in\left[0;\dfrac{1}{5}\right]\Rightarrow\left\{{}\begin{matrix}y_{min}=0\\y_{max}=\dfrac{1}{5}\end{matrix}\right.\)
HP
20 tháng 9 2021
6.
\(y=sinx+cosx+2=\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)+2\)
\(sin\left(x+\dfrac{\pi}{4}\right)\in\left[-1;1\right]\Rightarrow y=\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)+2\in\left[-\sqrt{2}+2;\sqrt{2}+2\right]\)
\(\Rightarrow y_{min}=-\sqrt{2}+2\)
\(y_{max}=\sqrt{2}+2\)
12 tháng 1 2022
Những người giáo viên được ví như những người lái đò cần cù và giàu tình yêu thương. Là một người học sinh, em đã được gặp gỡ không ít người lái đò vĩ đại. Nhưng người để lại ấn tượng sâu đậm nhất trong em chính là cô Hòa Bình.
Cô ấy là giáo viên dạy tiếng anh của em năm từ năm lớp 3 cho đến nay. Cô Bình có chiều cao chỉ khoảng 150cm, nặng chừng 45kg. Ai cũng nói là có vóc dáng nhỏ bé, nhí nhảnh. Điều đặc biệt là cô có nước da trắng rất đẹp, dù đi nắng suốt mấy buổi huấn luyện ngoài trời cũng chẳng bị đen đi. Khuôn mặt cô bầu bĩnh, kết hợp với đôi mắt đen to tròn khiến ai cũng nghĩ cô vẫn là sinh viên. Cô Bình suốt ba năm nay vẫn luôn để một kiểu tóc là mái tóc nâu uốn xoăn một chút ở đuôi. Kết hợp với các bộ áo dài màu tươi sáng khiến cô thật là dịu dàng và nữ tính.
Tuy nhiên, đó không phải là điều khiến em yêu quý cô hơn hẳn các thầy cô khác. Điều khiến cô chinh phục được bao thế hệ học sinh là trái tim ấm áp, đầy tình yêu thương của cô. Cô luôn đối xử bình đẳng với mọi học trò của mình. Dù gia đình điều kiện thế nào, bạn ấy học có giỏi không. Từng tiết học, em luôn cảm nhận được sự tâm huyết của cô. Từng trò chơi, video, hình ảnh, bộ câu hỏi… của cô đưa ra luôn mới mẻ và thu hút chúng em học tập. Ai cũng được trao cơ hội được nói, được phát biểu để rèn luyện bản thân hơn. Đặc biệt, cô không bao giờ ngần ngại khi dành thêm thời gian cuối buổi để giảng thêm bài cho chúng em. Chính nhân cách tuyệt vời ấy của cô đã khiến em và rất nhiều bạn học sinh khác kính trọng.
Hiện tại, em đang học những tháng cuối cùng với cô Bình. Vì sang năm tới, em sẽ chuyển sang một ngôi trường mới. Tuy nhiên, những tình cảm và kiến thức mà cô đã gửi gắm, em sẽ mang theo mãi và không bao giờ quên.
Bài văn tả cô
Cô giáo chủ nhiệm của lớp em là cô Lê Trà - một giáo viên giỏi và tốt bụng. Ngay từ lần đầu gặp cô là em đã rất yêu quý cô rồi.
Cô Lê Trà năm nay khoảng gần năm mươi tuổi, cũng đã gắn bó với nghề dạy học suốt hơn hai mươi năm nay rồi. Cô cao chừng mét sáu, thân hình thon gọn, mảnh mai. Với nước da trắng hồng, mái tóc đen truyền thống dài đến giữa lưng, trông cô thật là dịu dàng và đằm thắm. Cô Trà có đôi mắt đẹp lắm, đen láy và trong veo như nước hồ mùa thu. Đôi môi cô đỏ hồng, tươi tắn. Hai bên tai luôn đeo chiếc khuyên tai ngọc trai suốt bao năm không thay đổi. Trang phục đi dạy của cô là những chiếc áo dài xinh xắn, thướt tha với nhiều màu sắc và họa tiết khác nhau. Trong đó, cô đặc biệt yêu thích hơn cả là màu thiên thanh.
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 4 2021
Đặt \(\int f\left(x\right)dx=F\left(x\right)\Rightarrow\int\limits^{17}_1f\left(x\right)dx=F\left(17\right)-F\left(1\right)\)
Từ giả thiết:
\(2x.f\left(x^2+1\right)+\dfrac{f\left(\sqrt{x}\right)}{2\sqrt{x}}=2lnx\)
Lấy nguyên hàm 2 vế:
\(F\left(x^2+1\right)+F\left(\sqrt{x}\right)=2xlnx-2x+C\)
Thay \(x=4\):
\(F\left(17\right)+F\left(2\right)=16ln2-8+C\) (1)
Thay \(x=1\):
\(F\left(2\right)+F\left(1\right)=-2+C\) (2)
Trừ vế cho vế (1) cho (2):
\(F\left(17\right)-F\left(1\right)=16ln2-6\)
Vậy \(\int\limits^{17}_1f\left(x\right)dx=16ln2-6\)
NH
2
6 tháng 3 2023
1: vecto AC=(-2;2)
=>VTCP là (-2;2); vtpt là (2;2)
2: vecto AB=(-10;-2)=(5;1)
=>VTPT của Δ là (5;1)
vtcp của Δ là (-1;5)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 3 2023
\(\overrightarrow{AC}=\left(-2;2\right)=2\left(-1;1\right)\) nên đường thẳng AC nhận \(\left(-1;1\right)\) là 1 vtcp và \(\left(1;1\right)\) là 1 vtpt
b.
\(\overrightarrow{BA}=\left(10;2\right)=2\left(5;1\right)\) ; mà \(\Delta\perp AB\) nên \(\Delta\) nhận (5;1) là 1 vtpt và \(\left(1;-5\right)\) là 1 vtcp
30 tháng 1 2016
bạn chỉ cần tách x4-1 thành (x2-1)(x2+1),rồi đặt x2=t là ok