tìm tất cả các số nguyên x,y nguyên sao cho
x-2xy+y=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
Nguyễn Lê Phước Thịnh
8 tháng 4
Đúng(1)
Những câu hỏi liên quan
MP
1
11 tháng 12 2021
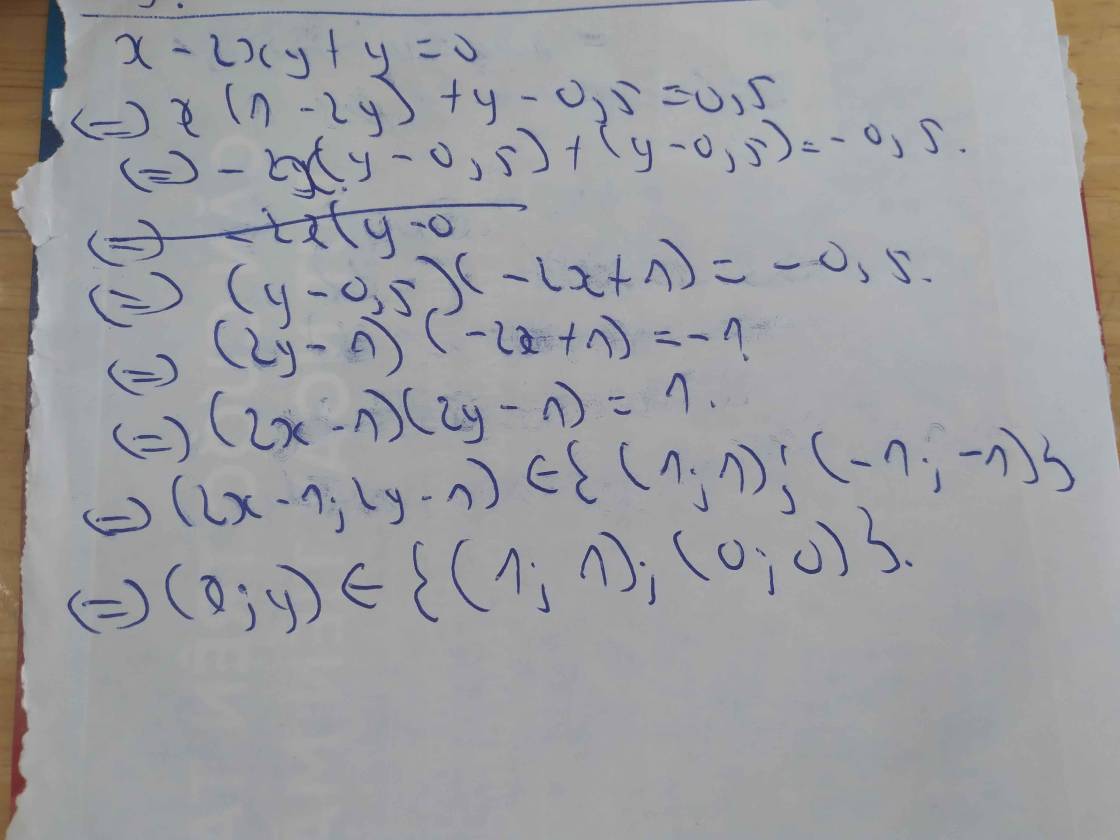
\(\Rightarrow2x-4xy+2y=0\\ \Rightarrow2x\left(1-2y\right)+2y-1=-1\\ \Rightarrow2x\left(1-2y\right)-\left(1-2y\right)=-1\\ \Rightarrow\left(2x-1\right)\left(2y-1\right)=1=1.1=\left(-1\right)\left(-1\right)\)
Với \(\left\{{}\begin{matrix}2x-1=1\\2y-1=1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\rightarrow\left(1;1\right)\)
Với \(\left\{{}\begin{matrix}2x-1=-1\\2y-1=-1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=0\\y=0\end{matrix}\right.\rightarrow\left(0;0\right)\)
Vậy các cặp \(\left(x;y\right)\) cần tìm là \(\left(1;1\right);\left(0;0\right)\)
T
2
T
1
13 tháng 5 2021
x+2xy+2y+6=0
x . (1 + 2y) + 2y + 6 = 0
x . (1 + 2y) + 2y + 1 = 5
(1 + 2y) . (x + 1) = 5
Phần còn lại làm đc nốt chưa
NH
1
DD
Đoàn Đức Hà
Giáo viên
16 tháng 1 2021
\(x-2xy+y=0\)
\(\Leftrightarrow2x-4xy+2y=0\)
\(\Leftrightarrow2x\left(1-2y\right)-\left(1-2y\right)=-1\)
\(\Leftrightarrow\left(2x-1\right)\left(1-2y\right)=-1=1.\left(-1\right)=\left(-1\right).1\)
Từ đây ta thế các trường hợp vào làm ra kết quả cuối cùng là: \(\left(x,y\right)\in\left\{\left(0,0\right),\left(1,1\right)\right\}\).
VN
1
DD
Đoàn Đức Hà
Giáo viên
15 tháng 1 2022
\(2xy+6x-3y-22=0\)
\(\Leftrightarrow2x\left(y+3\right)-3y-9=13\)
\(\Leftrightarrow\left(2x-3\right)\left(y+3\right)=13\)
Vì \(x,y\)là các số nguyên nên \(2x-3,y+3\)là các ước của \(13\).
Ta có bảng giá trị:
| 2x-3 | -13 | -1 | 1 | 13 |
| y+3 | -1 | -13 | 13 | 1 |
| x | -5 | 1 | 2 | 8 |
| y | -4 | -16 | 10 | -2 |
NM
1
26 tháng 5 2022
\(2xy-x-y=3\Leftrightarrow x\left(2y-1\right)-y=3\Leftrightarrow-2x\left(2y-1\right)+2y=-6\Leftrightarrow-2x\left(2y-1\right)+2y-1=-7\Leftrightarrow\left(1-2x\right)\left(2y-1\right)=-7\)Đến đây do x,y nguyên nên bạn lập bảng để tìm ra x,y nhá
LH
0
HQ
3
29 tháng 11 2018
phương trình tương đương với:
2x-4xy+2y-1= -1
=>(2x-1).(1-2y)= -1
=>(2x-1)(2y-1)=1 tìm được 2 cặp giá trị là \(\orbr{\begin{cases}x=y=0\left(tm\right)\\x=y=2\left(tm\right)\end{cases}}\)
29 tháng 11 2018
\(x-2xy+y=0\)
\(\Rightarrow x-(2xy-y)=0\)
\(\Rightarrow x-y(2x-1)=0\)
\(\Rightarrow2x-2y(2x-1)=0\)
\(\Rightarrow(2x-1)-2y(2x-1)=-1\)
\(\Rightarrow(2x-1)(1-2y)=-1\)
\(\Rightarrow(2x-1;1-2y)=(-1;1);(1;-1)\)
\(\Rightarrow(x,y)=(0,0);(1,1)\)
Vậy : ....
NT
21 tháng 7 2018
Ta có: 2xy + x - 2y = 4
=> 2y(x - 1) + x = 4
=> 2y(x - 1) + x - 1 = 3
=> 2y(x - 1) + (x - 1) = 3
=> (x - 1).(2y + 1) = 3
=> x-1 và 2y+1 là Ư(3)={-3;-1;1;3}
Ta có bảng:
| x - 1 | -1 | -3 | 1 | 3 |
| 2y + 1 | -3 | - 1 | 3 | 1 |
| x | 0 | -2 | 2 | 4 |
| y | -2 | -1 | 1 | 0 |
LC
3
NH
28 tháng 6 2020
Ta có :
2xy + x - 2y = 4
\(\Rightarrow\) 2y ( x - 1 ) + x = 4
\(\Rightarrow\) 2y ( x - 1 ) + x - 1 = 3
\(\Rightarrow\) 2y ( x - 1 ) + ( x - 1 ) = 3
\(\Rightarrow\) ( x - 1 ) . ( 2y + 1 ) = 3
\(\Rightarrow\) x - 1 và 2y + 1 là Ư(3) = { - 3 ; - 1 ; 1 ; 3 }
Ta có bảng :
| x - 1 | - 1 | - 3 | 1 | 3 |
| 2y + 1 | - 3 | - 1 | 3 | 1 |
| x | 0 | - 2 | 2 | 4 |
| y | - 2 | - 1 | 1 | 0 |
Vậy ...
28 tháng 6 2020
2xy+x-2y=4
x(2y+1)-2y=4
x(2y+1)-2y-1=3
x(2y+1)-(2y+1)=3
(x-1)(2y+1)=3
Vì x;y là số nguyên => x-1;2y+1 là số nguyên
=> x-1;2y+1 
Ta có bảng:
| x-1 | 1 | 3 | -3 | -1 |
| 2y+1 | 3 | 1 | -1 | -3 |
| x | 2 | 4 | -2 | 0 |
| y | 1 | 0 | -1 | -2 |
Vậy cặp số nguyên (x;y) cần tìm là: (2;1) ; (4;0) ; (-2;-1) ; (0;-2).