Bài 31: Cho tam giác ABC vuông tại A. Điểm D thuộc cạnh AB. Đường tròn đường kính BD cắt BC tại E. Các đường thẳng CD, AE lần lượt cắt đường tròn tại F, G.
a) Chứng minh rằng hai tam giác ABC và EBD đồng dạng với nhau.
b) Chứng minh rằng tứ giác ADEC nội tiếp được. c) Chứng minh rằng các đường thẳng AC, DE, BF đồng quy.
d) Khi D di chuyển trên đoạn thẳng AB thì F di chuyển trên đường nào?...
Đọc tiếp
Bài 31: Cho tam giác ABC vuông tại A. Điểm D thuộc cạnh AB. Đường tròn đường kính BD cắt BC tại E. Các đường thẳng CD, AE lần lượt cắt đường tròn tại F, G. a) Chứng minh rằng hai tam giác ABC và EBD đồng dạng với nhau. b) Chứng minh rằng tứ giác ADEC nội tiếp được. c) Chứng minh rằng các đường thẳng AC, DE, BF đồng quy. d) Khi D di chuyển trên đoạn thẳng AB thì F di chuyển trên đường nào? e) Cho BA=8cm, CA=6cm. Tính thể tích khối hình tạo bởi tam giác ABC quay quanh cạnh AB
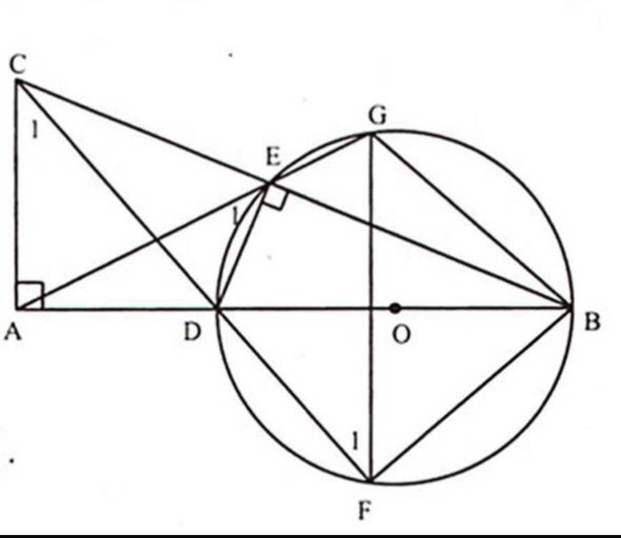
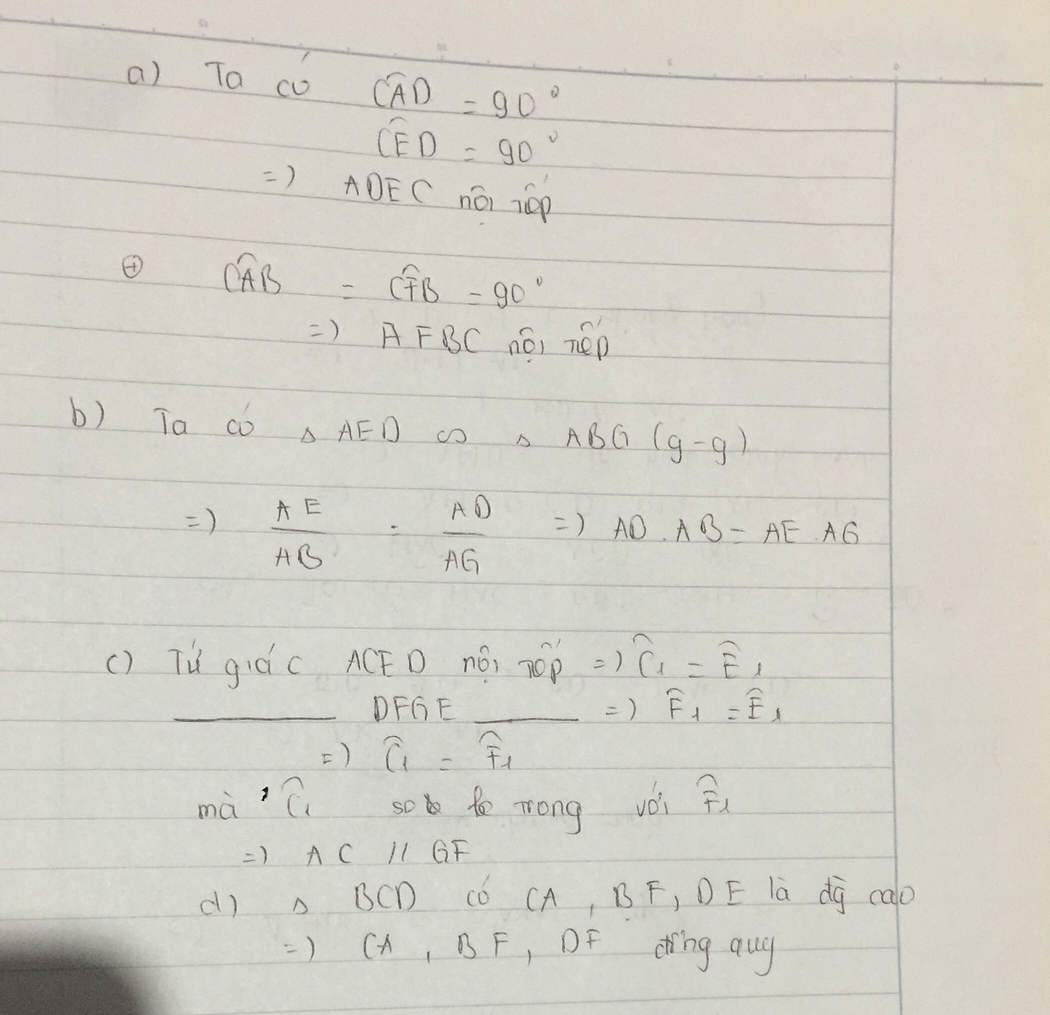
a: Gọi O là trung điểm của BD
=>O là tâm đường tròn đường kính BD
Xét (O) có
ΔBED nội tiếp
BD là đường kính
Do đó: ΔBED vuông tại E
=>DE\(\perp\)BC tại E
Xét ΔBED vuông tại E và ΔBAC vuông tại A có
\(\widehat{EBD}\) chung
Do đó: ΔBED~ΔBAC
b: Xét tứ giác ADEC có \(\widehat{DAC}+\widehat{DEC}=90^0+90^0=180^0\)
nên ADEC là tứ giác nội tiếp
c: Gọi H là giao điểm của BF và AC
Xét (O) có
ΔBFD nội tiếp
BD là đường kính
Do đó;ΔBFD vuông tại F
=>CF\(\perp\)BH tại F
Xét ΔHBC có
CF,BA là các đường cao
CF cắt BA tại D
Do đó: D là trực tâm của ΔHBC
=>HD\(\perp\)BC
mà DE\(\perp\)BC
và HD,DE có điểm chung là D
nên H,D,E thẳng hàng
=>CF,BA,DE đồng quy