tìm x biết: 1+1/3+1/6+1/10+...+2/x.(x+1)=1.2023/2025
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a, 2\(^3\) . x + 2005\(^0\) . x = 994-15:3+1\(^{2025}\)
8 .x + 1 . x = 990
x . [ 8 +1 ] = 990
x . 9 = 990
x = 990 : 9
x = 110

a) (x + 1) + (x + 2) + (x + 3) + (x + 4) + (x + 5) = 2025
(x + x + x + x + x) + (1 + 2 + 3 + 4 + 5) = 2025
5x + 15 = 2025
5x = 2025 - 15
5x = 2010
x = 2010 : 5
x = 402
b) 5 * x - x = 2020
5 * x - x * 1 = 2020
x * (5 - 1) = 2020
x * 4 = 2020
x = 2020 : 4
x = 505
mong bạn tick
a) ( x + 1 ) + ( x + 2) + ( x + 3 ) + ( x + 4 ) + ( x + 5 ) = 2025
\(\left(x+x+x+x+x\right)+\left(1+2+3+4+5\right)=2025\)
\(5x+15=2025\)
\(5x=2025-15\)
\(5x=2010\)
\(x=2010:5\)
\(x=402\).

1. Giải:
Do \(5x+13B\in\left(2x+1\right)\Rightarrow5x+13⋮2x+1.\)
\(\Rightarrow2\left(5x+13\right)⋮2x+1\Rightarrow10x+26⋮2x+1.\)
\(\Rightarrow5\left(2x+1\right)+21⋮2x+1.\)
Do 5(2x+1)⋮2x+1⇒ Ta cần 21⋮2x+1.
⇒ 2x+1 ϵ B(21)=\(\left\{1;3;7;21\right\}.\)
Ta có bảng:
| 2x+1 | 1 | 3 | 7 | 21 |
| x | 0 | 1 | 3 | 10 |
| TM | TM | TM | TM |
Vậy xϵ\(\left\{0;1;3;10\right\}.\)
2. Giải:
Do (2x-18).(3x+12)=0.
⇒ 2x-18=0 hoặc 3x+12=0.
⇒ 2x =18 3x =-12.
⇒ x =9 x =-4.
Vậy xϵ\(\left\{-4;9\right\}.\)
3. S= 1-2-3+4+5-6-7+8+...+2021-2022-2023+2024+2025.
S= (1-2-3+4)+(5-6-7+8)+...+(2021-2022-2023+2024)+2025 Có 506 cặp.
S= 0 + 0 + ... + 0 + 2025.
⇒S= 2025.

(1+2+3+4+5+6+7+8+9+...............................+2016+2025) x (24,2 - 24,2) = (1 + 2 +3+4+5+6+7+8+9+...............................+2016+2025) x 0 = 0

( x + 1 ) 3 – ( x – 1 ) 3 – 6 ( x – 1 ) 2 = - 10 ⇔ x 3 + 3 x 2 + 3 x + 1 – ( x 3 – 3 x 2 + 3 x – 1 ) – 6 ( x 2 – 2 x + 1 ) = - 10 ⇔ x 3 + 3 x 2 + 3 x + 1 – x 3 + 3 x 2 – 3 x + 1 – 6 x 2 + 12 x – 6 = - 10
ó 12x – 4 = -10
ó 12x = -10 + 4
ó 12x = -6
ó x = - 1 2
Đáp án cần chọn là: A

a: \(\left(2^3\right)^{1^{2005}}\cdot x+2005^0\cdot x=9915:3+1^{2025}\)
=>\(8\cdot x+1\cdot x=3305+1\)
=>\(9x=3306\)
=>\(x=\dfrac{3306}{9}=\dfrac{1102}{3}\)
b: \(2^x+2^{x+1}+2^{x+2}+2^{x+3}=480\)
=>\(2^x+2^x\cdot2+2^x\cdot4+2^x\cdot8=480\)
=>\(2^x\left(1+2+4+8\right)=480\)
=>\(2^x\cdot15=480\)
=>\(2^x=32\)
=>\(2^x=2^5\)
=>x+5
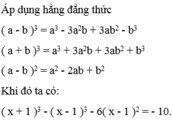
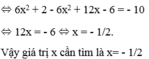
Sửa đề: \(1+\dfrac{1}{3}+\dfrac{1}{6}+...+\dfrac{2}{x\left(x+1\right)}=1-\dfrac{2023}{2025}\)
=>\(\dfrac{2}{2}+\dfrac{2}{6}+...+\dfrac{2}{x\left(x+1\right)}=\dfrac{2}{2025}\)
=>\(\dfrac{1}{2}+\dfrac{1}{6}+...+\dfrac{1}{x\left(x+1\right)}=\dfrac{1}{2025}\)
=>\(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{x\left(x+1\right)}=\dfrac{1}{2025}\)
=>\(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{x}-\dfrac{1}{x+1}=\dfrac{1}{2025}\)
=>\(1-\dfrac{1}{x+1}=\dfrac{1}{2025}\)
=>\(\dfrac{1}{x+1}=\dfrac{2024}{2025}\)
=>\(x+1=\dfrac{2025}{2024}\)
=>\(x=\dfrac{1}{2024}\)