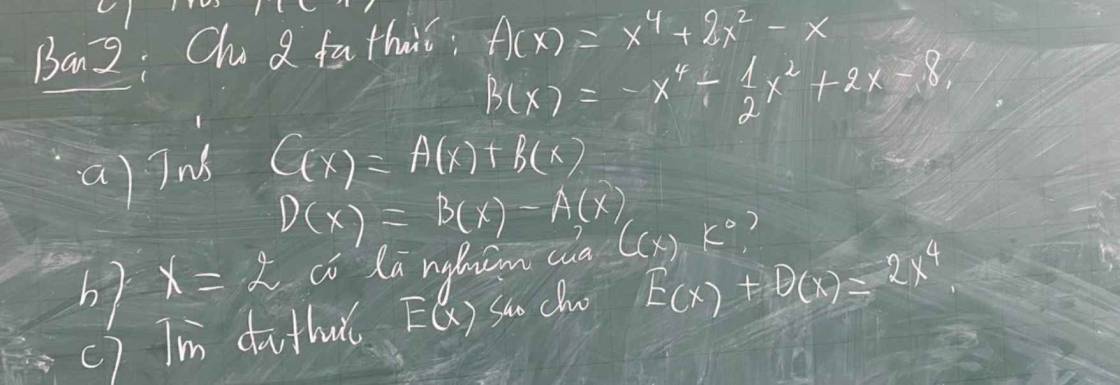 giúp mình vs cần gấp
giúp mình vs cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, khi K mở \(=>\left(R1ntR2\right)\)\(nt\left(R4//R5\right)\)
A2 chỉ 0,5 A\(=>I4=I\left(A2\right)=0,5A=>U4=U5=I4.R4=0,5.80\)\(=40V\)
\(=>I5=\dfrac{U5}{R5}=\dfrac{40}{20}=2A=>I45=I4+I5=2+0,5=2,5A\)\(=Im=I12\)=>số chỉ ampe kế(A1)=2,5A
\(=>R12=R1+R2=4+4=8\left(Om\right)\)
\(=>U12=I12.R12=8.2,5=20V\)\(=>UAB=U12+U4=60V\)
b,khi đóng K\(=>R1nt\left\{[R2nt\left(R4//R5\right)]//R3\right\}\)
\(=>R245=R2+\dfrac{R4.R5}{R4+R5}=4+\dfrac{80.20}{80+20}=20\left(om\right)\)
\(=>R2345=\dfrac{R3.R245}{R3+R345}=\dfrac{5.20}{5+20}=4\left(om\right)\)
\(=>Rtd=R1+R2345=4+4=8\left(om\right)\)
\(=>Im=\dfrac{UAB}{Rtd}=\dfrac{60}{8}=7,5A=I1=I2345\)
\(=>A1\) chỉ 7,5 A
\(=>U2345=I2345.R2345=7,5.4=30V\)\(=U245=U3\)
\(=>I245=\dfrac{U245}{R245}=\dfrac{30}{20}=1,5A=I45\)
\(=>U45=I45.R45=16.1,5=24V=U4\)
\(=>I4=\dfrac{U4}{R4}=\dfrac{24}{80}=0,3A\)\(=>A2\) chỉ 0,3A

1.Câu thơ trích trong bài thơ Nhớ Rừng.Tác giả Thế Lữ,các PTBĐ là biểu cảm(gián tiếp)
2.Thể thơ 8 tiếng


a) \(\dfrac{-15}{-2023}=\dfrac{15}{2023}>0\)
\(\dfrac{3}{-4}< 0\)
\(\Rightarrow\dfrac{-15}{-2023}>\dfrac{3}{-4}\)
b) \(\dfrac{2014}{-2015}< 0\)
\(\dfrac{-5}{-7}=\dfrac{5}{7}>0\)
\(\Rightarrow\dfrac{2014}{-2015}< \dfrac{-5}{-7}\)
c) \(\dfrac{-4162}{3976}< 0\)
\(\dfrac{1}{2}>0\)
\(\Rightarrow\dfrac{-4162}{3976}< \dfrac{1}{2}\)
d) \(\dfrac{-2401}{7693}< 0\)
\(\dfrac{-4}{-7}=\dfrac{4}{7}>0\)
\(\Rightarrow\dfrac{-2401}{7693}< \dfrac{4}{7}\)
a: \(\dfrac{-15}{-2023}=\dfrac{15}{2023}>0\)
\(\dfrac{3}{-4}< 0\)
Do đó: \(\dfrac{-15}{-2023}>\dfrac{3}{-4}\)
b: \(\dfrac{2014}{-2015}< 0\)
\(\dfrac{-5}{-7}=\dfrac{5}{7}>0\)
Do đó: \(\dfrac{2014}{-2015}< \dfrac{-5}{-7}\)
c: \(-\dfrac{4162}{3976}< 0\)
\(0< \dfrac{1}{2}\)
Do đó: \(-\dfrac{4162}{3976}< \dfrac{1}{2}\)
d: \(\dfrac{-2401}{7693}< 0\)
\(0< \dfrac{4}{7}=\dfrac{-4}{-7}\)
Do đó: \(-\dfrac{2401}{7693}< \dfrac{-4}{-7}\)
e: -17<-4
=>\(\dfrac{-17}{2019}< \dfrac{-4}{2019}\)
=>\(\dfrac{17}{-2019}< \dfrac{-4}{2019}\)
g: \(\dfrac{-15}{-43}=\dfrac{15}{43}\)
mà 15>7
nên \(\dfrac{-15}{-43}=\dfrac{15}{43}>\dfrac{7}{43}\)
h: \(\dfrac{-15}{60}=\dfrac{-15\cdot3}{60\cdot3}=\dfrac{-45}{180}\)
\(\dfrac{-20}{45}=\dfrac{-20\cdot4}{45\cdot4}=\dfrac{-80}{180}\)
Ta có: -45>-80
=>\(-\dfrac{45}{180}>-\dfrac{80}{180}\)
=>\(-\dfrac{15}{60}>-\dfrac{20}{45}\)
k: \(\dfrac{11}{45}>0\)
\(0>-\dfrac{14}{30}\)
Do đó: \(\dfrac{11}{45}>-\dfrac{14}{30}\)
m: \(-\dfrac{17}{15}< -\dfrac{15}{15}=-1\)
\(-1< -\dfrac{5}{18}=\dfrac{5}{-18}\)
Do đó: \(\dfrac{-17}{15}< \dfrac{5}{-18}\)
n: \(-\dfrac{14}{42}< 0\)
\(0< \dfrac{-56}{-28}\)
Do đó: \(\dfrac{-14}{42}< \dfrac{-56}{-28}\)


a) Ta có: \(Q=\dfrac{3x+\sqrt{9x}-3}{x+\sqrt{x}-2}-\dfrac{\sqrt{x}+1}{\sqrt{x}+2}+\dfrac{\sqrt{x}-2}{1-\sqrt{x}}\)
\(=\dfrac{3x+3\sqrt{x}-3-\left(x-1\right)-\left(x-4\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{3x+3\sqrt{x}-3-x+1-x+4}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x+3\sqrt{x}+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
b) Thay \(x=4+2\sqrt{3}\) vào Q, ta được:
\(Q=\dfrac{\sqrt{3}+1+1}{\sqrt{3}+1-1}=\dfrac{2+\sqrt{3}}{\sqrt{3}}=\dfrac{2\sqrt{3}+3}{3}\)
c) Để Q=3 thì \(\sqrt{x}+1=3\sqrt{x}-3\)
\(\Leftrightarrow\sqrt{x}-3\sqrt{x}=-3-1\)
\(\Leftrightarrow2\sqrt{x}=4\)
hay x=4
d) Để \(Q>\dfrac{1}{2}\) thì \(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{1}{2}>0\)
\(\Leftrightarrow\dfrac{2\sqrt{x}+2-\sqrt{x}+1}{2\left(\sqrt{x}-1\right)}>0\)
\(\Leftrightarrow\sqrt{x}-1>0\)
\(\Leftrightarrow x>1\)
Kết hợp ĐKXĐ, ta được: x>1
e) Để Q nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-1\)
\(\Leftrightarrow2⋮\sqrt{x}-1\)
\(\Leftrightarrow\sqrt{x}-1\in\left\{-1;1;2\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{0;2;3\right\}\)
hay \(x\in\left\{0;4;9\right\}\)

Cơ chế hình thành cây có kiểu gen Aaa là do rồi loạn giảm phân, diễn ra ở kì sau của giảm phân 1.
Sơ đồ lai:
P: Aa x Aa
GP: Aa ; 0 ; A ; a
F1: Aaa ; a
 giúp mình vs mình cần gấp
giúp mình vs mình cần gấp
 giúp mình vs mình cần gấp
giúp mình vs mình cần gấp



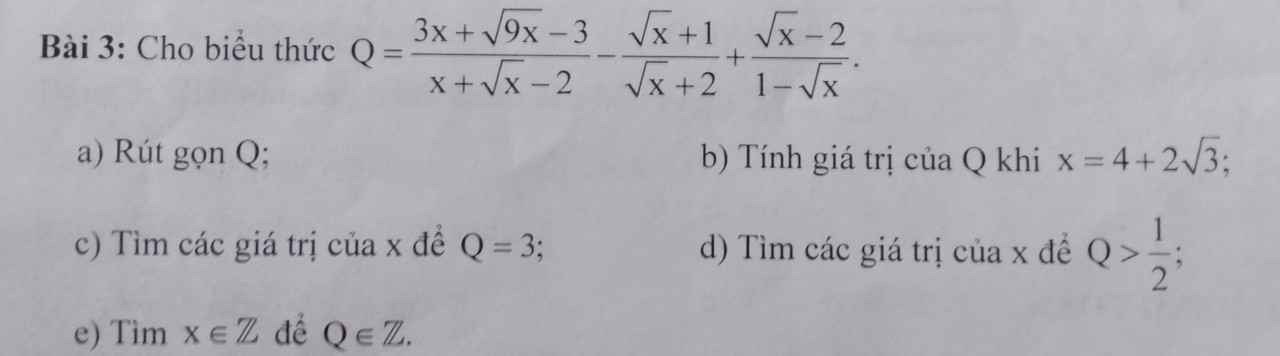 giúp mình vs mình đg cần gấp
giúp mình vs mình đg cần gấp 
Có: \(A\left(x\right)=x^4+2x^2-x\) và \(B\left(x\right)=-x^4-\dfrac{1}{2}x^2+2x-8\)
+, \(C\left(x\right)=A\left(x\right)+B\left(x\right)\)
\(=\left(x^4+2x^2-x\right)+\left(-x^4-\dfrac{1}{2}x^2+2x-8\right)\)
\(=x^4+2x^2-x-x^4-\dfrac{1}{2}x^2+2x-8\)
\(=\dfrac{3}{2}x^2+x-8\)
+, \(D\left(x\right)=B\left(x\right)-A\left(x\right)\)
\(=\left(-x^4-\dfrac{1}{2}x^2+2x-8\right)-\left(x^4+2x^2-x\right)\)
\(=-x^4-\dfrac{1}{2}x^2+2x-8-x^4-2x^2+x\)
\(=-2x^4-\dfrac{5}{2}x^2+3x-8\)
b) Ta có: \(C\left(x\right)=\dfrac{3}{2}x^2+x-8\)
\(\Rightarrow C\left(2\right)=\dfrac{3}{2}\cdot2^2+2-8=0\)
\(\Rightarrow x=2\) là 1 nghiệm của \(C\left(x\right)\)
c) Có: \(E\left(x\right)+D\left(x\right)=2x^4\)
\(\Rightarrow E\left(x\right)=2x^4-D\left(x\right)\)
\(=2x^4-\left(-2x^4-\dfrac{5}{2}x^2+3x-8\right)\)
\(=2x^4+2x^4+\dfrac{5}{2}x^2-3x+8\)
\(=4x^4+\dfrac{5}{2}x^2-3x+8\)