chọn ngẫu nhiên 8 lá bài trong cỗ bài gồm 32 lá. Tính xác suất để được ít nhất 3 lá già
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
Gọi \(A\) là biến cố “Hạt giống thứ nhất nảy mầm”, \(B\) là biến cố “Hạt giống thứ hai nảy mầm”.
\(P\left( A \right) = P\left( B \right) = 0,8 \Rightarrow P\left( {\bar A} \right) = P\left( {\bar B} \right) = 1 - 0,8 = 0,2\)
Xác suất để có đúng 1 trong 2 hạt giống đó nảy mầm là:
\(P\left( {A\bar B} \right) + P\left( {\bar AB} \right) = P\left( A \right).P\left( {\bar B} \right) + P\left( {\bar A} \right).P\left( B \right) = 0,8.0,2 + 0,2.0,8 = 0,32\)
CY
1
SV
Sinh Viên NEU
CTVVIP
6 tháng 10 2023
\(n_{\left(\Omega\right)}=3!=6\)
Gọi biến cố đối A1 : Không có lá thư nào đúng người nhận
\(\Rightarrow n_{\left(A_1\right)}=2\)
\(\Rightarrow P_{\left(A\right)}=1-P_{\left(A_1\right)}=1-\dfrac{2}{6}=\dfrac{2}{3}\)
AH
Akai Haruma
Giáo viên
12 tháng 8 2023
Lời giải:
Rút 5 trong 52 lá bài, có $C^5_{52}$ kết quả.
Rút 5 lá 10, J, Q, K, A đồng chất, có 4 kết quả (bích, tép, cơ, rô)
Xác suất rút được 5 lá thỏa mãn đề: $\frac{4}{C^5_{52}}$
HP
30 tháng 8 2021
Gọi A là biến cố "Rút được 2 lá bài cơ".
Số kết quả thuận lợi là \(\left|\Omega_A\right|=C^2_{13}=78\).
Số kết quả có thể xảy ra là \(\left|\Omega\right|=C^2_{52}=1326\).
\(\Rightarrow\) Xác suất xảy ra biến cố A là \(P\left(A\right)=\dfrac{78}{1326}=\dfrac{1}{17}\).
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
- Số phần tử của không gian mẫu là: \(n\left( \Omega \right) = 3! = 6\)
- Gọi B là biến cố “Không lá thư nào được bỏ đúng phong bì”
A là biến cố “Có ít nhất một lá thư được bỏ đúng phong bì”
⇨ n(B) = 2
⇨ \(P(A) = 1 - P(B) = 1 - \frac{2}{6} = \frac{2}{3}\)
DT
1
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 12 2020
Không gian mẫu: \(C_{52}^2\)
Số cách rút không có quân K nào: \(C_{48}^2\)
Xác suất: \(P=\dfrac{C_{52}^2-C_{48}^2}{C_{52}^2}=...\)
CM
16 tháng 7 2019
Đáp án A
Phương pháp giải: Áp dụng nguyên lý bù trừ trong bài toán xác suất
Lời giải:
Ta tính xác suất để xảy ra không một lá thư nào đúng địa chỉ.
Mỗi phong bì có 4 cách bỏ thư vào nên có tất cả 4! cách bỏ thư.
Gọi U là tập hợp các cách bỏ thư và Am là tính chất lá thư thứ m bỏ đúng địa chỉ.
Khi đó, theo công thức về nguyên lý bù trừ, ta có N ¯ = 4 ! - N 1 + N 2 - . . . + ( - 1 ) 4 N 4 .
Trong đó Nm ( 1 ≤ m ≤ 4 ) là số tất cả các cách bỏ thư sao cho có m lá thư đúng địa chỉ.
Nhận xét rằng, Nm là tổng theo mọi cách lấy m lá thư từ 4 lá, với mỗi cách lấy m lá thư, có (4 - m)! cách bỏ m lá thư này đúng địa chỉ, ta nhận được:
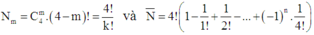
Suy ra xác suất cần tìm cho việc không lá thư nào đúng địa chỉ là
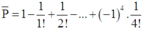
Vậy xác suất để có ít nhất 1 lá thư bỏ đúng phong bì của nó là P = 1 - P ¯ = 5 8 .
CM
29 tháng 3 2018
Đáp án A
Phương pháp giải: Áp dụng nguyên lý bù trừ trong bài toán xác suất
Lời giải:
Ta tính xác suất để xảy ra không một lá thư nào đúng địa chỉ.
Mỗi phong bì có 4 cách bỏ thư vào nên có tất cả 4! cách bỏ thư.
Gọi U là tập hợp các cách bò thư và A m là tính chất lá thư thứ m bỏ đúng địa chỉ.
Khi đó, theo công thức về nguyên lý bù trừ, ta có N ¯ = 4 ! − N 1 + N 2 − ... + − 1 4 N 4
Trong đó N m 1 ≤ m ≤ 4 là số tất cả các cách bỏ thư sao cho có m lá thư đúng địa chỉ.
Nhận xét rằng, N m là tổng theo mọi cách lấy m lá thư từ 4 lá, với mỗi cách lấy m lá thư, có 4 − m ! cách bỏ m lá thư này đúng địa chỉ, ta nhận được: N m = C 4 m . 4 − m ! = 4 ! k ! và
N ¯ = 4 ! 1 − 1 1 ! + 1 2 ! − ... + − 1 n . 1 4 !
Suy ra xác suất cần tìm cho việc không lá thư nào đúng địa chỉ là P ¯ = 1 − 1 1 ! + 1 2 ! − ... + − 1 4 . 1 4 !
Vậy xác suất để có ít nhất 1 lá thư bỏ đúng phong bì của nó là P = 1 − P ¯ = 5 8
CM
28 tháng 12 2019
Đáp án C
Bỏ 4 lá thư vào 4 phong bì ta có số cách bỏ là.
4! Cách.
Ta xét các trường hợp sau.
TH1: chỉ có một lá thư bỏ đúng. giải sử ta chọn 1 trong 4 lá để bỏ đúng (có 4 cách), trong mỗi cách đó chọn một lá để bỏ sai (có 2 cách), khi đó 2 lá còn lại nhất thiết là sai (1 cách), vậy trong TH1 này có 4.2.1=8 cách.
TH2: có đúng 2 lá bỏ đúng. Tương tự trên, ta chọn 2 lá bỏ đúng (có 6 cách), 2 lá còn lại nhất thiết sai (1 cách), vậy trong TH2 này có 6 cách.
TH3: dễ thấy khi 3 lá đã bỏ đúng thì đương nhiên là cả 4 lá đều đúng, vậy có 1 cách.
Suy ra có 8+6+1=15 cách bỏ ít nhất có 1 lá thư vào đúng địa chỉ.
Vậy xác suất cần tìm là: 15/24=5/8
CM
6 tháng 11 2018
Đáp án C
Bỏ 4 lá thư vào 4 phong bì ta có số cách bỏ là. 4! Cách
Ta xét các trường hợp sau.
TH1: chỉ có một lá thư bỏ đúng.giải sử ta chọn 1 trong 4 lá để bỏ đúng (có 4 cách)
trong mỗi cách đó chọn một lá để bỏ sai (có 2 cách)
khi đó 2 lá còn lại nhất thiết là sai (1 cách)
vậy trong TH1 này có 4.2.1=8 cách.
TH2: có đúng 2 lá bỏ đúng
Tương tự trên, ta chọn 2 lá bỏ đúng (có C 4 2 = 6 cách)
2 lá còn lại nhất thiết sai (1 cách), vậy trong TH2 này có 6 cách.
TH3: dễ thấy khi 3 lá đã bỏ đúng thì đương nhiên là cả 4 lá đều đúng, vậy có 1 cách.
Suy ra có 8 + 6 +1 = 15 cách bỏ ít nhất có 1 lá thư vào đúng địa chỉ.
Vậy xác suất cần tìm là: 15 24 = 5 8
Chắc bạn ghi nhầm đề, bộ bài 52 lá chứ ko phải 32 lá
Không gian mẫu: \(C_{52}^8\)
Số cách chọn để được ít nhất 3 lá già là:
\(C_4^3.C_{48}^5+C_4^4.C_{48}^4\)
Xác suất: \(P=\dfrac{C_4^3.C_{48}^5+C_4^4.C_{48}^4}{C_{52}^8}\)