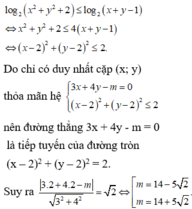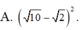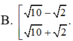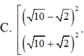tìm tất cả các cặp x y nguyên thỏa mãn (x-y)2 = 4y2 +2x+4y+2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
0
GK
0
NN
1
NY
6 tháng 8 2020
Để cho gọn, đặt {x2=ay2=b
(a+4b+28)2−17a2−17b2=238b+833
\(\Leftrightarrow\)a2+16b2+784+8ab+56a+224b−17a2−17b2=238b+833
\(\Leftrightarrow\)16a2+b2+49−8ab−56a+14b=0
\(\Leftrightarrow\)(4a−b−7)2=0 ⇔4a−b−7=0⇔4x2−y2−7=0
\(\Leftrightarrow\)(2x−y)(2x+y)=7
Do 2x+y>2x−y với mọi x, y nguyên dương và 2x+y>0 với mọi x, y nguyên dương
\(\Rightarrow\){2x−y=12x+y=7 \(\Rightarrow\){x=2y=3
Vậy pt có cặp nghiệm nguyên dương duy nhất (x;y)=(2;3)
#Shinobu Cừu
GC
4
CM
1 tháng 5 2019
Chọn C.
Phương pháp: Đưa bài toán về tìm m để hệ có nghiệm duy nhất.
23 tháng 12 2016
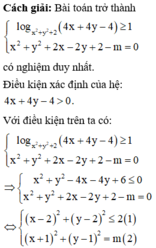
Mình gợi ý phần đầu nè. Xét \(x=0\) riêng được \(y=0\) hoặc \(y=1\).
Xét \(x\ne0\). Khi đó \(x\) và \(x^2+x+1\) nguyên tố cùng nhau với mọi \(x\) nguyên khác 0.
(Ở đây ta chỉ định nghĩa 2 số nguyên tố cùng nhau là 2 số có ước chung lớn nhất là 1 nên số âm vẫn được).
Để CM điều này ta gọi \(d=gcd\left(x^2+x+1,x\right)\) thì \(1⋮d\).
Vế trái là một số chia hết cho 4 nên trong 2 số \(x\) và \(x^2+x+1\) phải có một số chia hết cho 4
(Nếu mỗi số đều chia hết cho 2 thì không thể nguyên tố cùng nhau)
Trường hợp 1: \(x⋮4\) còn \(x^2+x+1\) lẻ.
Do \(y\) và \(y-1\) có 1 số chẵn và 1 số lẻ nên số chẵn sẽ là ước của \(x\) còn số lẻ là ước của \(x^2+x+1\).
Tức là có 2 trường hợp: \(x=4y\) và \(x=4\left(y-1\right)\).
Trường hợp 2 ngược lại.
Tới đây bạn tự giải được nha.
23 tháng 12 2016
\(x\left[1+x+x^2\right]=4y\left[y-1\right]\)
\(\Leftrightarrow x^3+x^2-4y^2+x+4y=0\)
\(\Leftrightarrow x^2\left[x+1\right]+x-4y^2+4y=0\)
\(\Leftrightarrow\Delta=b^2-4ac=1-16xy+16xy^2-16y+16y^2\)
\(\Rightarrow\orbr{\begin{cases}x1=\frac{-1+\sqrt{1-16xy+16xy^2-16y+16y^2}}{2x+2}\\x2=\frac{-1-\sqrt{1-16xy+16xy^2-16y+16y^2}}{2x+2}\end{cases}}\)
đến đây tự làm tiếp nhé
KV
1
9 tháng 9 2020
Xét \(x=0\Rightarrow y^2=-2y\Leftrightarrow\orbr{\begin{cases}y=0\\y=-2\end{cases}}\)
Xét \(x\ne0\Rightarrow x^2\ge1\)(vì \(x\inℤ\))
\(2x^2-2xy+y^2=2\left(x-y\right)\Leftrightarrow x^2+\left(x^2-2xy+y^2\right)-2\left(x-y\right)=0\)
\(\Leftrightarrow x^2+\left(x-y\right)^2-2\left(x-y\right)=0\)
Vì \(x^2\ge1\)nên \(x^2+\left(x-y\right)^2-2\left(x-y\right)\ge\left(x-y\right)^2-2\left(x-y\right)+1=\left(x-y-1\right)^2\ge0\)
Mà đề yêu cầu giải biểu thức bằng 0 nên ta xét điều kiện xảy ra của dấu "=": \(\hept{\begin{cases}x^2=1\\x-y-1=0\end{cases}}\)
\(\orbr{\begin{cases}x=1,y=0\\x=-1,y=-2\end{cases}}\)
\(\hept{\begin{cases}x^2=1\\x-y-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}\hept{\begin{cases}x=1\\y=0\end{cases}}\\\hept{\begin{cases}x=-1\\y=-2\end{cases}}\end{cases}}}\)Vậy phương trình nhận 4 nghiệm (x;y)=(0;0),(0;-2),(1;0),(-1;-2).