so sánh hai số biết
a) a=1+3+3^2+3^3+...+3^6 và b=3^7-1
b) c=1+2+2^2+2^3+....+2^2002 và d=2^2003-1
Giai ra chi tiết
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
M
20 tháng 9 2017
a,
A=1+3+32+33+34+35+36
=> 3A=3+32+33+34+35+36+37
=> 3A-A=(3+32+33+34+35+36+37)-(1+3+32+33+34+35+36)
=> 2A=37-1
=> A=37-1/2
Vì (37-1)/2 < 37-1
=> A < B
b, C=1+2+22+...+22001+22002
=> 2C=2+22+23+....+22002+22003
=> 2C-C=(2+22+23+...+22002+22003)-(1+2+22+...+22002)
=> C=22003-1
Vì 22003-1 = 22003-1
=> C = D.
20 tháng 9 2017
a) \(A=1+3+3^2+...+3^6\)
\(\Rightarrow3A=3+3^2+...+3^7\)
\(\Rightarrow3A-A=3+3^2+...+3^7-1-3-3^2-...-3^6\)
\(\Rightarrow2A=3^7+2\)
\(\Rightarrow A=\frac{3^7+2}{2}\)
Vì \(3^7-1>\frac{3^7+2}{2}\)=> A < B.
b) Câu này thì nhân C cho 2 và làm tương tự như câu trên nha.
M
2
B
11 tháng 5 2019
A = 1 + 2 + 22 + 23 + ... + 22002
=> 2A = 2 + 22 + 23 + 24 + ... + 22003
=> 2A - A = ( 2 + 22 + 23 + 24 + ... + 22003 ) - ( 1 + 2 + 22 + 23 + ... + 22002 )
A = 22003 - 1 < 22003
hay A < B
Vậy ...
11 tháng 5 2019
\(A=1+2+2^2+2^3+...+2^{2002}\)
\(\Rightarrow2A=2+2^2+2^3+...+2^{2002}+2^{2003}\)
\(\Rightarrow2A-A=2^{2003}-1\)
\(\Rightarrow A=2^{2003}-1\)
Vì \(2^{2003}-1< 2^{2003}\)
nên A < B
T
9 tháng 6 2018
1) Áp dụng BĐT \(\frac{a}{b}>\frac{a-m}{b-m}\) với \(\frac{a}{b}< 1\) .Dễ dàng chứng minh Bđt trên, áp dụng vào ta có:
a) \(x=\frac{2002}{2003}=\frac{2002-1+1}{2003-1+1}=\frac{2003-1}{2004-1}< \frac{2003}{2004}\)
Với \(\frac{a}{b}=\frac{2003}{2004};\frac{a-m}{b-m}=\frac{2003-1}{2004-1}\)
Từ đó ta có: x < y
b) Vì đây là phân số âm nên bé hơn phân số dương nên ta có BĐT: \(\frac{a}{b}>\frac{c}{d}\Leftrightarrow\frac{-a}{b}< \frac{-c}{d}\)
Áp dụng vào bài toán trên với \(\frac{a}{b}=\frac{2002}{2003}< 1\)và \(\frac{c}{d}=\frac{2005}{2004}>1\)
Nên \(\frac{a}{b}< \frac{c}{d}\Leftrightarrow\frac{-a}{b}>\frac{-c}{d}\)hay x > y
IA
9 tháng 6 2018
Bài 1 :
a, Ta có : \(x=\frac{2002}{2003}=1-\frac{1}{2003}\)
\(y=\frac{2003}{2004}=1-\frac{1}{2004}\)
Vì \(\frac{1}{2003}>\frac{1}{2004}\)
\(\Rightarrow1-\frac{1}{2003}< 1-\frac{1}{2004}\)
\(\Rightarrow x< y\)
b, Ta thấy cả 2 vế đều có dấu âm nên ta rút gọn dấu âm đi thì được :
\(x=\frac{2002}{2003}\) \(y=\frac{2005}{2004}\)
Lúc này :
Ta có : \(y=\frac{2005}{2004}>1=\frac{2003}{2003}>\frac{2002}{2003}=x\)
Vì khi so sánh dương sẽ đối ngược với so sánh âm :
\(\Rightarrow\)Khi trả lại dấu âm thì tất nhiên \(x=\frac{-2002}{2003}>y=\frac{2005}{-2004}\)
Vậy \(x>y\)
Bài 2 :
Ta quy đồng các phân số trên như sau :
\(\frac{-2}{7}=\frac{-6}{21}\) \(\frac{-2}{9}=\frac{-6}{27}\)
Gọi các phân số thỏa mãn điều kiện trên là x .
Ta có : \(\frac{-6}{21}< x< \frac{-6}{27}\)
\(\Rightarrow x\in\left\{\frac{-6}{22};\frac{-6}{23};\frac{-6}{24};\frac{-6}{25};\frac{-6}{26}\right\}\)
Ta rút gọn và dấu của các phân số như sau ( nếu không rút gọn được thì cúng đừng chuyển dấu ) :
\(x\in\left\{\frac{3}{-11};\frac{-6}{23};\frac{3}{-12};\frac{-6}{25};\frac{3}{-13}\right\}\)
Vậy các phân số thỏa mãn đề bài là : \(\frac{3}{-11};\frac{3}{-12};\frac{3}{-13}\).
7 tháng 7 2015
A = 1 + 2 + 2² + ... + 2^2002
A = 1 + (2 + 2² + ... + 2^2002 )
Ta xét :
u1 = 2
u2 = 2.2 = 22
u3 = 2.22 = 2^3
u2002 = 2.2^2001 = 2^2002
Tổng cấp số nhân : S = u1.(1 - q^n) / (1 - q) = 2.(1 - 2^2002) / (1 - 2) = 2(2^2002 - 1) = 2^2003 - 2
A = 1 + 2^2003 - 2 = 2^2003 - 1
So sánh với B
2^2003 - 1 = 2^2003 - 1
Vậy B = A
VN
24 tháng 1 2017
Bài 1: Quy đồng => so sánh => trả về phân số ban đầu
Bài 2: Như bài 1
14 tháng 10 2021
Bài 1
a) 4/3 < 1/3
b) 2/5 < 3/2
c) 7/2 > 1/4
d) 3/4 < 5/6
Bài 2
a) 6/10 = 3/5 và 4/5 vậy 3/5 < 4/5
b) 3/4 và 6/12 = 1/2 vậy 3/4 > 1/2
a ) Ta có:
A = 1 + 3 + 32 + 33+ ..... + 36
A x 3 = 3 + 32 + 33 + 34 + .... + 37
A x 2 - A = ( 3 + 32 + 33 + 34 + .... + 37 ) - ( 1 + 3 + 32 + 33 + .... + 36 )
A = 37 - 1
Mà : B = 37 - 1 nên A = B
b ) Ta có :
C = 1 + 2 + 22 + 23 + ...... + 22002
C x 2 = 2 + 22 + 23 + 24 + ..... + 22003
C x 2 - C = ( 2 + 22 + 23 + 24 + ...... + 22003 ) - ( 1 + 2 + 22 + 23 + ..... + 22002 )
C = 22003 - 1
Mà : D = 22003 - 1 nên C = D
A=1+3+3^2+....+3^100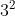
+
+...+
+
+
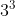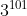
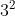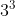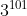)-(1+3+
+....+
)
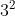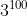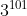-1
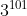-1):2
\Rightarrow 3A=3+
\Rightarrow3A-A=2A=(3+
=
\RightarrowA=(