Rút gọn biểu thức -9(x^2+7x-2)+(3x-1)(3x+1)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H9
HT.Phong (9A5)
CTVHS
14 tháng 4 2023
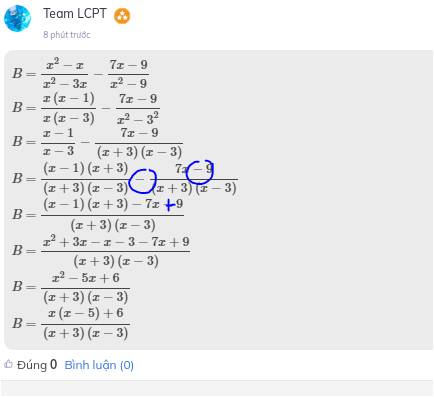
\(B=\dfrac{x^2-x}{x^2-3x}-\dfrac{7x-9}{x^2-9}\)
\(B=\dfrac{x\left(x-1\right)}{x\left(x-3\right)}-\dfrac{7x-9}{x^2-3^2}\)
\(B=\dfrac{x-1}{x-3}-\dfrac{7x-9}{\left(x+3\right)\left(x-3\right)}\)
\(B=\dfrac{\left(x-1\right)\left(x+3\right)}{\left(x+3\right)\left(x-3\right)}-\dfrac{7x-9}{\left(x+3\right)\left(x-3\right)}\)
\(B=\dfrac{\left(x-1\right)\left(x+3\right)-7x-9}{\left(x+3\right)\left(x-3\right)}\)
\(B=\dfrac{x^2+3x-x-3-7x+9}{\left(x+3\right)\left(x-3\right)}\)
\(B=\dfrac{x^2-5x+6}{\left(x+3\right)\left(x-3\right)}\)
\(B=\dfrac{x\left(x-5\right)+6}{\left(x+3\right)\left(x-3\right)}\)
16 tháng 3 2023
\(a,-3x^2+7x-9+\left(x-1\right)\left(x+2\right)\\ =-3x^2+7x-9+x^2-x+2x-2\\ =\left(-3x^2+x^2\right)+\left(7x-x+2x\right)-\left(9+2\right)\\ =-2x^2+8x-11\\ b,x\left(x-5\right)-2x\left(x+1\right)\\ =x^2-5x-2x^2-2x\\ =\left(x^2-2x^2\right)-\left(5x+2x\right)\\ =-3x^2-7x\\ c,4x\left(x^2-x+1\right)-\left(x-1\right)\left(x^2-x\right)\\ =4x^3-4x^2+4x-x\left(x^2-x\right)+x^2-x\\ =4x^3-4x^2+4x-x^3+x^2+x^2-x\\ =\left(4x^3-x^3\right)+\left(-4x^2+x^2+x^2\right)+\left(4x-x\right)\\ =3x^3-2x^2+3x\\ =x\left(3x^2-2x+3\right)\)
\(d,-5x\left(x-5\right)+\left(x-3\right)\left(x^2-7\right)\\ =-5x^2+25x+x\left(x^2-7\right)-3\left(x^2-7\right)\\ =-5x^2+25x+x^3-7x-3x^2+21\\ =\left(-5x^2-3x^2\right)+\left(25x-7x\right)+x^3+21\\ =-8x^2+x^3+18x+21\)
NL
1
TH
31 tháng 12 2020
(\(3+\dfrac{x}{3-x}+\dfrac{2x}{3+x}-\dfrac{4x^2-3x-9}{x^2-9}\) ):\(\left(\dfrac{2}{3-x}-\dfrac{x-1}{3x-x^2}\right)\)\(=\left(\dfrac{3x^2-27}{\left(x-3\right)\left(x+3\right)}+\dfrac{-x\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}+\dfrac{2x\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}-\dfrac{4x^2-3x-9}{\left(x-3\right)\left(x+3\right)}\right)\)\(:\left(\dfrac{2x}{x\left(3-x\right)}-\dfrac{x-1}{x\left(3-x\right)}\right)\)
\(=\dfrac{3x^2-27-x^2-3x+2x^2-6x-4x^2+3x+9}{\left(x-3\right)\left(x+3\right)}:\dfrac{x+1}{x\left(3-x\right)}\)
\(=\dfrac{-6x-18}{\left(x-3\right)\left(x+3\right)}:\dfrac{x+1}{x\left(3-x\right)}\) \(=\dfrac{-6\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}:\dfrac{x+1}{x\left(3-x\right)}\)
\(=\dfrac{6}{3-x}.\dfrac{x\left(x-3\right)}{x+1}\) \(=\dfrac{6x}{x+1}\)
29 tháng 6 2023
a: =12x^4-6x^3+3x+4x^3-2x^2+1
=12x^4-2x^3-2x^2+3x+1
b: =14x^4+28x^2+6x^2+12x
=14x^4+34x^2+12x
29 tháng 6 2023
`@` `\text {Ans}`
`\downarrow`
\((3x + 1)(4x³ - 2x² + 1)\)
`= 3x(4x^3-2x^2+1) + 4x^3 - 2x^2 + 1`
`= 12x^4 - 6x^3 + 3x + 4x^3 - 2x^2 + 1`
`= 12x^4 + (-6x^3 + 4x^3) - 2x^2 + 3x + 1`
`= 12x^4 - 2x^3 - 2x^2 + 3x + 1`
\((7x² + 3x)(2x + 4)\)
`= 7x^2(2x+4) + 3x(2x+4)`
`= 14x^3 + 28x^2 + 6x^2 + 12x`
`= 14x^3 + (28x^2 + 6x^2)+12x`
`= 14x^3 + 34x^2 + 12x`
`@` `\text {Kaizuu lv uuu}`
24 tháng 6 2021
a) \(2x\left(5-3x^2\right)-10\left(6+x\right)\)
\(=10x-6x^3-60-10x\)
\(=\) \(-6x^3-60\)
PT
24 tháng 6 2021
a) \(2x\left(5-3x^2\right)-10\left(6+x\right)\\ =2x.5-2x.3x^2-10.6-10.x\\ =10x-6x^3-60-10x\)
b) \(3\left(-x+2\right)-6\left(1-x+5x^{20}\right)\\ =-3.x+3.2-6.1+6.x-5.5x^{20}\\ =-3x+6-6+6x-25x^{20}=25x^{20}+3x\)
c) \(7x\left(2-5x^2+\dfrac{1}{2}x^3\right)-14x\left(1-2x^2\right)\\ =7x.2-7x.5x^2+7x.\dfrac{1}{2}x^3-14x.1+14x.2x^2\\ =14x-25x^3+\dfrac{7}{2}x^4-14x+28x^3=3x^2+\dfrac{7}{2}x^4\)
18 tháng 4 2021
a, ĐK : \(x\ne1;2;3;4;5\)
b, \(\dfrac{1}{x\left(x-1\right)}+\dfrac{1}{\left(x-1\right)\left(x-2\right)}+\dfrac{1}{\left(x-2\right)\left(x-3\right)}+\dfrac{1}{\left(x-3\right)\left(x-4\right)}+\dfrac{1}{\left(x-4\right)\left(x-5\right)}\)
\(=\dfrac{1}{x}-\dfrac{1}{x-1}+\dfrac{1}{x-1}-\dfrac{1}{x-2}+\dfrac{1}{x-2}-\dfrac{1}{x-3}+\dfrac{1}{x-3}-\dfrac{1}{x-4}+\dfrac{1}{x-4}-\dfrac{1}{x-5}\)
\(=\dfrac{1}{x}-\dfrac{1}{x-5}=\dfrac{x-5-x}{x\left(x-5\right)}=\dfrac{-5}{x\left(x-5\right)}\)