Hãy nhắc lại công thức xác định tích vô hướng của hai vectơ trong mặt phẳng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 9 2018
Tích vô hướng của hai vec tơ a→ và b→:
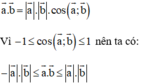
+ a→.b→ đạt giá trị lớn nhất bằng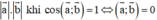 
⇔ a→ và b→ cùng hướng.
+ a→.b→ đạt giá trị nhỏ nhất bằng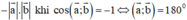 
⇔ a→ và b→ ngược hướng.
PT
1
CM
9 tháng 5 2017
Từ giả thiết suy ra a → = 4 ; 6 và b → = 3 ; − 7 .
Suy ra a → . b → = 4.3 + 6. − 7 = − 30.
Chọn A.
VT
20 tháng 2 2019
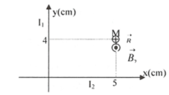
b) Gọi N là điểm có vectơ cảm ứng từ gây bởi hai dòng điện bằng 0, ta có N phải thuộc góc phần tư thứ nhất và thứ ba
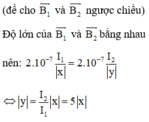
Vì N thuộc góc phần tư thứ nhất và thứ ba nên x, y cùng dấu, suy ra y = 5x
Vậy tập hợp những điểm có vectơ cảm ứng từ gây bởi hai dòng điện bằng 0 là đường thẳng y = 5x
30 tháng 3 2017
\(\overrightarrow{a}\) . \(\overrightarrow{b}\) = ( -3) . 2 + 1.2 = -4
HQ
Hà Quang Minh
Giáo viên
27 tháng 9 2023
Khoảng cách hai điểm M,I (hay độ dài đoạn thẳng MI) chính là độ dài vecto \(\overrightarrow {MI} \)
\(\overrightarrow {MI} = \left( {a - x;b - y} \right) \Rightarrow \left| {\overrightarrow {MI} } \right| = \sqrt {{{\left( {a - x} \right)}^2} + {{\left( {;b - y} \right)}^2}} \)
Vậy khoảng cách giữa hai điểm \(I\left( {a;b} \right)\) và \(M\left( {x;y} \right)\) là \(\sqrt {{{\left( {a - x} \right)}^2} + {{\left( {;b - y} \right)}^2}} \)
HQ
Hà Quang Minh
Giáo viên
30 tháng 9 2023
a) Ta có: \(\overrightarrow {OM} = \left( {2;1} \right),\overrightarrow {MN} = \left( { - 3;2} \right),\overrightarrow {MP} = \left( {2;1} \right)\)
b) Ta có: \(\overrightarrow {MN} .\overrightarrow {MP} = - 3.2 + 2.1 = - 4\)
c) Ta có: \(MN = \left| {\overrightarrow {MN} } \right| = \sqrt {{{\left( { - 3} \right)}^2} + {2^2}} = \sqrt {13} ,MP = \left| {\overrightarrow {MP} } \right| = \sqrt {{2^2} + {1^2}} = \sqrt 5 \)
d) Ta có: \(\cos \widehat {MNP} = \frac{{\overrightarrow {MN} .\overrightarrow {MP} }}{{\left| {\overrightarrow {MN} } \right|.\left| {\overrightarrow {MP} } \right|}} = \frac{- 4}{{\sqrt {13} .\sqrt 5 }} = \frac{- 4}{{\sqrt {65} }}\)
e) Tọa độ trung điểm I của đoạn NP là: \(\left\{ \begin{array}{l}{x_I} = \frac{{{x_N} + {x_P}}}{2} = \frac{3}{2}\\{y_I} = \frac{{{y_N} + {y_P}}}{2} = \frac{5}{2}\end{array} \right. \Leftrightarrow I\left( {\frac{3}{2};\frac{5}{2}} \right)\)
Tọa độ trọng tâm G của tam giác MNP là: \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_M} + {x_N} + {x_P}}}{3}\\{y_G} = \frac{{{y_M} + {y_N} + {y_P}}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_G} = \frac{5}{3}\\{y_C} = 2\end{array} \right. \Leftrightarrow G\left( {\frac{5}{3};2} \right)\)
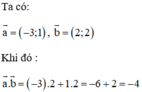
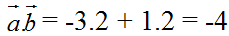
Công thức xác định tích vô hướng của hai vectơ trong mặt phẳng: Tích vô hướng của hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) là một số, kí hiệu là \(\overrightarrow u \cdot \overrightarrow v \), được xác định bởi công thức sau:
\(\overrightarrow u \cdot \overrightarrow v = \left| {\overrightarrow u } \right| \cdot \left| {\overrightarrow v } \right| \cdot \cos \left( {\overrightarrow u ,\overrightarrow v } \right)\).