Trong Ví dụ 8, gọi I là điểm thuộc đoạn thẳng AG sao cho \(\overrightarrow {AI} = 3\overrightarrow {IG} \) (H.2.19). Chứng minh rằng \(\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} = \overrightarrow 0 \).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 9 2019
Giả sử \(\frac{IA}{AB}=k\Rightarrow\frac{IB}{AB}=1-k\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{IA}=-k\overrightarrow{AB}\\\overrightarrow{IB}=\left(1-k\right)\overrightarrow{AB}\end{matrix}\right.\)
\(\Rightarrow IB.\overrightarrow{IA}+IA.\overrightarrow{IB}=\left(1-k\right).AB.\left(-k\right)\overrightarrow{AB}+k.AB.\left(1-k\right)\overrightarrow{AB}\)
\(=\left(k^2-k\right)AB.\overrightarrow{AB}+\left(k-k^2\right)AB.\overrightarrow{AB}\)
\(=\left(k^2-k+k-k^2\right).AB.\overrightarrow{AB}=\overrightarrow{0}\)
BT
16 tháng 5 2017
a) Giả sử điểm I thỏa mãn:
\(\overrightarrow{IA}+3\overrightarrow{IB}-2\overrightarrow{IC}=\overrightarrow{0}\)\(\Leftrightarrow\overrightarrow{IA}-\overrightarrow{IC}+\overrightarrow{IB}-\overrightarrow{IC}+2\overrightarrow{IB}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{CA}+\overrightarrow{CB}+2\overrightarrow{IB}=\overrightarrow{0}\)
\(\Leftrightarrow2\overrightarrow{IB}=\overrightarrow{AC}+\overrightarrow{BC}\)
\(\Leftrightarrow\overrightarrow{IB}=\dfrac{\overrightarrow{AC}+\overrightarrow{BC}}{2}\).
Xác định véc tơ: \(\dfrac{\overrightarrow{AC}+\overrightarrow{BC}}{2}\).
Dựng điểm B' sao cho \(\overrightarrow{BC}=\overrightarrow{CB'}\).
\(\overrightarrow{AC}+\overrightarrow{BC}=\overrightarrow{AC}+\overrightarrow{CB'}=\overrightarrow{AB'}\).
\(\dfrac{\overrightarrow{AC}+\overrightarrow{BC}}{2}=\dfrac{\overrightarrow{AB'}}{2}\).
Dựng điểm I sao cho \(\overrightarrow{IB}=\dfrac{\overrightarrow{AC}+\overrightarrow{BC}}{2}=\overrightarrow{AK}\) (K là trung điểm của AB').
BT
16 tháng 5 2017
b) Tìm điểm I sao cho: \(\overrightarrow{IA}+3\overrightarrow{IB}-2\overrightarrow{IC}=\overrightarrow{0}\) và chứng mịn điểm I cố định.
Có: \(\overrightarrow{IA}+3\overrightarrow{IB}-2\overrightarrow{IC}=\overrightarrow{IA}+3\overrightarrow{IB}+2\overrightarrow{CI}\)
\(=\left(\overrightarrow{CI}+\overrightarrow{IA}\right)+\left(\overrightarrow{CI}+\overrightarrow{IB}\right)+2\overrightarrow{IB}\)
\(=\overrightarrow{CA}+\overrightarrow{CB}+2\overrightarrow{IB}\).
Suy ra: \(\overrightarrow{CA}+\overrightarrow{CB}+2\overrightarrow{IB}=\overrightarrow{0}\)\(\Leftrightarrow\overrightarrow{IB}=\dfrac{\overrightarrow{AC}+\overrightarrow{BC}}{2}\)
Vậy điểm I xác định sao cho \(\overrightarrow{IB}=\dfrac{\overrightarrow{AC}+\overrightarrow{BC}}{2}\) .
Do A, B, C cố định nên tồn tại một điểm I duy nhất.
Theo giả thiết:
Có \(\overrightarrow{MN}=\overrightarrow{MA}+3\overrightarrow{MB}-2\overrightarrow{MC}\)\(=\overrightarrow{MI}+\overrightarrow{IA}+3\left(\overrightarrow{MI}+\overrightarrow{IB}\right)-2\left(\overrightarrow{MI}+\overrightarrow{IC}\right)\)
\(=2\overrightarrow{MI}+\overrightarrow{IA}+3\overrightarrow{IB}-2\overrightarrow{IC}\)
\(=2\overrightarrow{MI}\) (Do các xác định điểm I).
Vì vậy \(\overrightarrow{MN}=2\overrightarrow{MI}\) nên hai véc tơ \(\overrightarrow{MN},\overrightarrow{MI}\) cùng hướng.
Suy ra 3 điểm M, N, I thẳng hàng hay MN luôn đi qua điểm cố định I.
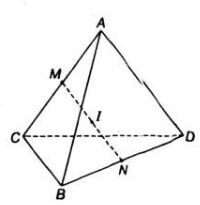
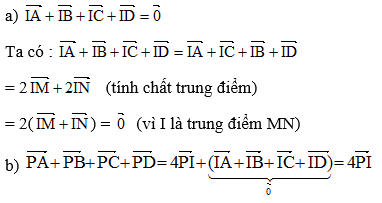
Theo ví dụ 8 ta có: \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 3\overrightarrow {AG} \)\( \Rightarrow \overrightarrow {AI} + \overrightarrow {IB} + \overrightarrow {AI} + \overrightarrow {IC} + \overrightarrow {AI} + \overrightarrow {ID} = 3\overrightarrow {AG} \)
\( \Rightarrow \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} = 3\overrightarrow {AG} - 3\overrightarrow {AI} = 3\left( {\overrightarrow {AG} + \overrightarrow {IA} } \right) = 3\overrightarrow {IG} = \overrightarrow {AI} \)\( \Rightarrow \overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} = \overrightarrow 0 \)