Cho B=5\(^0\)+5\(^1\)+5\(^2\)+...+5\(^{25}\)và so sanh với 5\(^{26}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
M
2
M
22 tháng 3 2018
ta có B <1
suy ra B=\(\frac{5^{26}+1}{5^{27}+1}\)<\(\frac{5^{26}+1+4}{5^{27}+1+4}\)<\(\frac{5^{26}+5}{5^{27}+5}\)=\(\frac{5\cdot\left(5^{25}+1\right)}{5\cdot\left(5^{26}+1\right)}\)=\(\frac{5^{25}+1}{5^{26}+1}\)=A
Vậy B<A
k cho mk nha
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
19 tháng 9 2015
\(26^{14}>25^{14}=\left(5^2\right)^{14}=5^{28}\)
\(5^{30}=\left(5^3\right)^{10}=125^{10}>124^{10}\)
\(4^{21}=\left(4^3\right)^7=64^7>64^2\)
\(27^{16}.16^9=\left(3^3\right)^{16}.\left(4^2\right)^9=3^{48}.4^{18}>12^{18}=3^{18}.4^{18}\)
\(31^{11}<32^{11}=\left(2^5\right)^{11}=2^{55}\)
\(17^{14}>16^{14}=\left(2^4\right)^{14}=2^{56}\)
\(2^{56}>2^{55}\) => \(17^{14}>31^{11}\)
Các bài khác làm tương tự
DT
1
13 tháng 9 2017
S=\(2^4+2^5+2^6+...+2^{25}\)
2S=\(2^5+2^6+2^7+...+2^{26}\)
2S-S=\(2^{26}-2^4\)
S=\(2^{26}-16\)
Vậy S<\(2^{26}-15\)
HH
1
27 tháng 4 2016
A=1+5+5^2+..+5^9/1+5+5^2+...+5^8
=1+5^9/1+5+5^2+...+5^8
B=1+3+3^2+..+3^9/1+3+3^2+..+3^8
=1+3^9/1+3+3^2+..+3^8
đặt A' =1+5+5^2+...+5^8
5A'=5+5^2+5^3+...+5^9
5A'-A'=5+5^2+5^3+...+5^9-5-1-5-5^2-...-5^8
4A'=5^9-1=>A'=(5^9-1):4
tương tự B'=(3^9-1):4
A=1+5^9/(5^9-1)/4=4.5^9/5^9-1
B=1+3^9/(3^9-1)/4=4.3^9/3^9-1
=> A<B
LN
2
28 tháng 8 2016
Bài 1 :
Ta có :
\(2\sqrt{5}-5-\left(\sqrt{5}-3\right)=\sqrt{5}-8=\sqrt{5}-\sqrt{64}< 0\)
\(\Rightarrow2\sqrt{5}-5< \sqrt{5}-3\)
Vậy ...
Bài 2 :
Ta có :
\(\sqrt{17}>\sqrt{16}\)
\(\sqrt{26}>\sqrt{25}\)
\(\Rightarrow\sqrt{17}+\sqrt{26}>\sqrt{16}+\sqrt{25}=4+5=9\)
Vậy ...
Bài 3 :
\(13\sqrt{35}=\sqrt{169}.\sqrt{35}>\sqrt{48}.\sqrt{1}=48\)
Vậy ...
HL
1
30 tháng 6 2017
a, Có 5^28 = (5^2) ^14
=25^14 < 26^14
b, Có 5^30 = (5^3) ^10)
=125^10 > 124^10
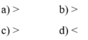
B = 5^0 + 5^1 + 5^2 + ... + 5^25 = 1 + 5 + 5^2 + ... + 5^25
5B = 5 + 5^2 + 5^3 + ... + 5^26
4B = ( 5 + 5^2 + 5^3 + ... + 5^26 ) - ( 1 + 5 + 5^2 + ... + 5^25 )
4B = 5^26 - 1
B = 5^26 - 1 / 4
Vậy B chắc chắn nhỏ hơn 5^26
B<5^26 vì B = 5^26 - 1