00< góc alpha < 900 . CMR : P=sin6alpha + cos6alpha + 3sin2alpha + cos2alpha không phụ vào giá trị góc alpha
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AT
30 tháng 7 2021
\(\left(\sqrt{\dfrac{1+sin\alpha}{1-sin\alpha}}+\sqrt{\dfrac{1-sin\alpha}{1+sin\alpha}}\right).\dfrac{1}{\sqrt{1+tan^2\alpha}}\)
\(=\left(\sqrt{\dfrac{\left(1+sin\alpha\right)^2}{\left(1-sin\alpha\right)\left(1+sin\alpha\right)}}+\sqrt{\dfrac{\left(1-sin\alpha\right)^2}{\left(1+sin\alpha\right)\left(1-sin\alpha\right)}}\right).\dfrac{1}{\sqrt{1+\left(\dfrac{sin\alpha}{cos\alpha}\right)^2}}\)
\(=\left(\sqrt{\dfrac{\left(1+sin\alpha\right)^2}{1-sin^2\alpha}}+\sqrt{\dfrac{\left(1-sin\alpha\right)^2}{1-sin^2\alpha}}\right).\dfrac{1}{\sqrt{\dfrac{cos^2\alpha+sin^2\alpha}{cos^2\alpha}}}\)
\(=\left(\sqrt{\dfrac{\left(1+sin\alpha\right)^2}{cos^2\alpha}}+\sqrt{\dfrac{\left(1-sin\alpha\right)^2}{cos^2\alpha}}\right).\dfrac{1}{\sqrt{\dfrac{1}{cos^2\alpha}}}\)
\(=\left(\dfrac{1+sin\alpha}{cos\alpha}+\dfrac{1-sin\alpha}{cos\alpha}\right).\dfrac{1}{\dfrac{1}{cos\alpha}}=\dfrac{2}{cos\alpha}.cos\alpha=2\)
27 tháng 8 2021
a/ \(A=\frac{cot^2a-cos^2a}{cot^2a}-\frac{sina.cosa}{cota}\)
\(=\frac{\frac{cos^2a}{sin^2a}-cos^2a}{\frac{cos^2a}{sin^2a}}-\frac{sina.cosa}{\frac{cosa}{sina}}\)
\(=\left(1-sin^2a\right)-sin^2a=1\)
27 tháng 8 2021
b/ \(B=\left(cosa-sina\right)^2+\left(cosa+sina\right)^2+cos^4a-sin^4a-2cos^2a\)
\(=cos^2a-2cosa.sina+sin^2a+cos^2a+2cosa.sina+sin^2a+\left(cos^2a+sin^2a\right)\left(cos^2a-sin^2a\right)-2cos^2a\)
\(=2+\left(cos^2a-sin^2a\right)-2cos^2a\)
\(=2-sin^2a-cos^2a=2-1=1\)
10 tháng 7 2016
Ta có: \(\sin^2\alpha+\cos^2\alpha=1\forall\alpha\)
\(\Rightarrow\left(\sin^2\alpha+\cos^2\alpha\right)^3=1\Rightarrow\sin^6\alpha+\cos^6\alpha+3\sin^2\alpha\cdot\cos^2\alpha\cdot\left(\sin^2\alpha+\cos^2\alpha\right)=1.\)
\(\Rightarrow E=\sin^6\alpha+\cos^6\alpha+3\sin^2\alpha\cdot\cos^2\alpha=1.\)không phụ thuộc vào \(\alpha\)
2 tháng 10 2015
\(A=\sin^2\alpha+\cos^2\alpha+2.\sin\alpha.\cos\alpha-2\sin\alpha.\cos\alpha-1\)
\(=1-1=0\) nên với mọi góc \(\alpha\) thì A không phụ thuộc vào \(\alpha\)
HQ
Hà Quang Minh
Giáo viên
25 tháng 8 2023
a, Do \(-1\le sin\alpha\le1\Rightarrow-0,3\le v_x=0,3sin\alpha\le0,3\)
Vậy giá trị lớn nhất của \(v_x\) là 0,3m/s và giá trị nhỏ nhất là -0,3m/s
b, Ta có đồ thị hàm số:
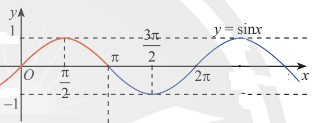
Với góc \(\alpha\in\left(0;\dfrac{\pi}{2}\right)\) hoặc \(\alpha\in\left(\dfrac{3\pi}{2};2\pi\right)\) thì \(v_x\) tăng.
13 tháng 4 2020
1) \(\left(\tan\alpha+\cot\alpha\right)^2-\left(\tan\alpha-\cot\alpha\right)^2\)
= \(\tan^2\alpha+\cot^2\alpha+2\tan\alpha.\cot\alpha-\tan^2\alpha+2\tan\alpha.\cot\alpha-\cot^2\alpha\)
= \(4\tan\alpha.\cot\alpha\)
= \(4.\frac{\cos\alpha}{\sin\alpha}.\frac{\sin\alpha}{\cos\alpha}=4\)
2) \(\frac{2-\sqrt{2+\sqrt{2+\sqrt{2}}}}{2-\sqrt{2+\sqrt{2}}}\)
= \(\frac{4-2-\sqrt{2+\sqrt{2}}}{\left(2+\sqrt{2+\sqrt{2+\sqrt{2}}}\right)\left(2-\sqrt{2+\sqrt{2}}\right)}\)
= \(\frac{1}{\left(2+\sqrt{2+\sqrt{2+\sqrt{2}}}\right)}\)
Mặt khác: \(\sqrt{2}< 2\Rightarrow2+\sqrt{2}< 4\Rightarrow2+\sqrt{2+\sqrt{2}}< 2+\sqrt{4}=4\)
=> \(2+\sqrt{2+\sqrt{2+\sqrt{2}}}< 2+\sqrt{4}=4\)
=> \(\frac{1}{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}>\frac{1}{4}\)
=> \(\frac{2-\sqrt{2+\sqrt{2+\sqrt{2}}}}{2-\sqrt{2+\sqrt{2}}}>\frac{1}{4}\)
VT
3 tháng 10 2018
\(A=\sin^6\alpha+cos^6\alpha+3\sin^2\alpha\cos^2\alpha\left(\sin^2\alpha+\cos^2\alpha\right).\)vì\(\sin^2\alpha+\cos^2\alpha=1\)
\(=\left(\sin^2\alpha+\cos^2\alpha\right)^3=1^3=1\)
\(B=2\left(\cos^2\alpha+\sin^2\alpha\right)=2.1=2\)
\(C=\frac{-4\cos\alpha\sin\alpha}{\sin\alpha\cos\alpha}=-4\)
để mình làm cho
\(P=\sin^6_a+\cos^6_a+3\sin_a^2+\cos^2_a=\left(\sin^2_a+\cos^2_a\right)\left(\sin^4_a-\sin^2_a\cos^2_a+\cos^4_a\right)\) \(+3.\sin^2_a.\cos^2_a\)
\(=\sin^4_a+2\sin^2_a.\cos^2_a+\cos^4_a=\left(\sin^2_a+\cos^2_a\right)^2=1\)
đề đoạn cuối phải là nhân chứ không phải +
ko phụ thuộc nhé