Chứng minh nếu A \(\subset\) B và B \(\subset\) A thì A = B
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tham khảo:
+) Biểu diễn: \(A \subset B\)
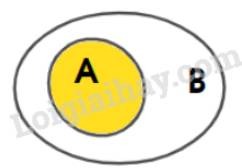
+) Sau đó, biểu diễn: \(B \subset C\)

Quan sát biểu đồ Ven, dễ thấy \(A \subset C.\)

Vì: \(a=b;b=c\Rightarrow a=c\)(tích chất bắt cầu)
\(\Rightarrow A\subset B;B\subset C\Rightarrow A\subset C\)
tíc mình nha
Chứng minh bằng hình vẽ :
A B C
Vòng tròn A nằm trong vòng tròn B,vòng tròn B nằm trong vòng tròn C nên vòng tròn A nằm trong vòng tròn C,suy ra đpcm.

Ta có A hợp B bằng B \(\Rightarrow\)A hiệu B bằng rỗng\(\Rightarrow\)\(\forall\)x\(\in\)A thì x\(\in\)B
Vậy A\(\subset\)B

Mệnh đề A sai
Phản ví dụ: vì C bất kì nên \(B\cap C\) có thể bằng rỗng, mà \(A\cap B=A\) nên nếu \(A\ne\varnothing\) thì \(A\cap B\) không phải con của \(B\cap C\)
\(A\subset B\Rightarrow\)tất cả các phần tử của A đều có trong tập hợp B
\(B\subset A\Rightarrow\)tất cả các phần tử của B đều có trong tập hợp A
=>A=B
=>đpcm
đương nhiên rồi sao phải c/m