Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E lần lượt là điểm đối xứng của H qua các cạnh AB, AC. a. Chứng minh BD // CE b. Chứng minh ACE ABC c. Chứng minh bd.cd = de^2 /4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét tứ giác AMHK có
góc AMH=góc AKH=góc KAM=90 độ
=>AMHK là hình chữ nhật
=>AH=MK
b: Xét ΔAHD có
AB vừa là đường cao, vừa là trung tuyến
nên ΔAHD cân tại A
=>AH=AD và AB là phân giác của góc HAD(1)
Xét ΔHEA có
AC vừa là đường cao, vừa là trung tuyến
nên ΔAHE cân tại A
=>AH=AE và AC là phân giác của góc HAE(2)
Từ (1), (2) suy ra góc DAE=2*90=180 độ
=>D,A,E thẳng hàng
mà AD=AE
nên A là trung điểm của DE
c: Xét ΔAHB và ΔADB có
AH=AD
góc HAB=góc DAB
AB chung
=>ΔAHB=ΔADB
=>góc ADB=90 dộ
=>BD vuông góc DE(3)
Xét ΔAHC và ΔAEC có
AH=AE
góc HAC=góc EAC
AC chung
=>ΔAHC=ΔAEC
=>goc AEC=90 độ
=>CE vuông góc ED(4)
Từ (3), (4) suy ra BD//CE

a: Ta có: D đối xứng H qua AB
=>AB là đường trung trực của HD
=>AH=AD và BH=BD
Xét ΔAHB và ΔADB có
AH=AD
BH=BD
AB chung
Do đó: ΔAHB=ΔADB
=>\(\widehat{HAB}=\widehat{DAB}\)
mà tia AB nằm giữa hai tia AH,AD
nên AB là phân giác của góc HAD
=>\(\widehat{HAD}=2\cdot\widehat{HAB}\)
Ta có: H đối xứng E qua AC
=>AH=AE và CH=CE
Xét ΔAHC và ΔAEC có
AH=AE
CH=CE
AC chung
Do đó: ΔAHC=ΔAEC
=>\(\widehat{HAC}=\widehat{EAC}\)
mà tia AC nằm giữa hai tia AH,AE
nên AC là phân giác của góc HAE
=>\(\widehat{HAE}=2\cdot\widehat{HAC}\)
Ta có: \(\widehat{HAD}+\widehat{HAE}=\widehat{EAD}\)
=>\(\widehat{EAD}=2\left(\widehat{HAB}+\widehat{HAC}\right)\)
=>\(\widehat{EAD}=2\cdot\widehat{BAC}=180^0\)
=>E,A,D thẳng hàng
Ta có: ΔAHB=ΔADB
=>\(\widehat{AHB}=\widehat{ADB}\)
=>\(\widehat{ADB}=90^0\)
=>BD\(\perp\)DE
Ta có: ΔAHC=ΔAEC
=>\(\widehat{AHC}=\widehat{AEC}\)
=>\(\widehat{AEC}=90^0\)
=>CE\(\perp\)ED
mà BD\(\perp\)DE
nên BD//CE
b: Ta có: \(\widehat{BAD}+\widehat{CAE}=\dfrac{1}{2}\left(\widehat{HAD}+\widehat{HAE}\right)\)
=>\(\widehat{BAD}+\widehat{CAE}=\dfrac{1}{2}\cdot180^0=90^0\)
mà \(\widehat{BAD}+\widehat{ABD}=90^0\)(ΔDAB vuông tại D)
nên \(\widehat{ABD}=\widehat{CAE}\)
Xét ΔABD vuông tại D và ΔCAE vuông tại E có
\(\widehat{ABD}=\widehat{CAE}\)
Do đó: ΔABD~ΔCAE

a: Xét tứ giác AKHM có
\(\widehat{AKH}=\widehat{AMH}=\widehat{MAK}=90^0\)
Do đó: AKHM là hình chữ nhật
Suy ra: AH=KM

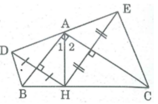
∆ ADB = ∆ AHB ⇒ BD = BH.
∆ AEC = ∆ AHC ⇒ CE = CH.
Vậy BD + CE = BH + CH = BC.

a) D,E đối xứng H qua AB,AC => AB,AC là trung trực của HD và HE
Dùng các tính chất của đường trung trực dễ dàng có \(\Delta ABH=\Delta ABD\)và \(\Delta ACH=\Delta ACE\)
=> \(\hept{\begin{cases}\widehat{BAD}=\widehat{BAH}\\\widehat{CAE}=\widehat{CAH}\end{cases}}\)Xét\(\widehat{DAE}=\widehat{BAD}+\widehat{BAH}+\widehat{CAE}+\widehat{CAH}=2\left(\widehat{BAH}+\widehat{CAH}\right)=2\widehat{BAC}=2.90^0=180^0\)
=>A,D,E thẳng hàng
b) Có \(\Delta ABH=\Delta ABD\)và \(\Delta ACH=\Delta ACE\)=>\(\hept{\begin{cases}\widehat{AEC}=\widehat{AHC}=90^0\\\widehat{ADB}=\widehat{AHB}=90^0\end{cases}}\)=>đpcm
c) Có \(\Delta ABH=\Delta ABD\)và \(\Delta ACH=\Delta ACE\)=>\(\hept{\begin{cases}BD=BH\\CE=CH\end{cases}\Rightarrow BD+CE=BH+CH=BC}\)

a) Theo tính chất một điểm nằm trên đường trung trực thì cách đều 2 đầu mút
=> AD = AH và AH = AE
Xét tam giác BDA và tam giác BHA có :
BA chung
BD = BH (theo tính chất nêu trên) => tam giác BDA = tam giác BHA (1)
AD = AH
Xét tam giác AHC và tam giác AEC có :
AC chung
AH = AE => tam giác AHC = tam giác AEC (2)
CH = CE (như tính chất nêu trên)
Từ (1)
=> \(AD⊥BD\) và \(\widehat{DAB}=\widehat{HAB}\)
Từ (2) ta cũng có :
\(AE⊥CE\) và \(\widehat{HAC}=\widehat{EAC}\)
Ta lại có :
\(\widehat{HAB}+\widehat{HAC}=90^0\)
\(\Rightarrow\widehat{DAB}+\widehat{HAB}+\widehat{HAC}+\widehat{EAC}=2\widehat{HAB}+2\widehat{HAC}=180^0\)
=> D , A , E thẳng hàng
VÀ AD vuông góc với BD
AE vuông góc với CE
MÀ AD , AE thuộc DE
=> BD // CE

a) Vì D là điềm đối xứng với H qua AB nên AB là đường trung trực của DH
=> AH=AD (1)
Vì E đối xứng với H qua AC nên AC là đường trung trực của HE
=> AH=AE (2)
Từ (1) và (2) suy ra AD=AE (3)
Mặt khác góc DAB=gócBAH; gócHAC= góc CAE và góc BAH+góc HAC=90o
do đó góc DAB+góc BAH+góc HAC+góc CAE=180o
=> D, A, E thẳng hàng (4)
từ (3) và (4) suy ra D và E đx với nhau qua A.
b) Tam giác DHE có HA là trung tuyến và HA= 1/2 DE
=> tam giác DHE vuông tại H.
c) Tam giác ADB=tam giác AHB (c-c-c)
suy ra góc ADB=góc AHB=90o
tương tự ta có : góc AEC=90o
suy ra BD//CE (cùng vuông góc với DE)
nên tứ giác BAEC là hình thang có 2 góc vuông kề cạnh bên DE
=> BAEC là hình thang vuông.
a) Vì D là điểm đối xứng với H qua AB nên AB là đường trung trực của DH
=> AH=AD (1)
Vì E đối xứng với H qua AC nên AC là đường trung trực của HE
=> AH=AE (2)
Từ (1) và (2) suy ra AD=AE (3)
Mặt khác góc DAB= góc BAH; góc HAC=góc CAE và góc BAH+góc HAC=90o
Do đó góc DAB + góc BAH+ góc HAC + góc CAE=180o
=> D, A, E thẳng hàng (4)
Từ (3) và (4) suy ra D và E đx với nhau qua A.
b) Tam giác DHE có HA là trung tuyến và HA= 1/2 DE
=> tam giác DHE vuông tại H.
c) Tam giác ADB=tam giác AHB (c-c-c)
suy ra góc ADB=góc AHB=90o
tương tự ta có góc AEC=90o
=> BD//CE (cùng vuông góc với DE)
nên tứ giác BDEC là hình thang có 2 góc vuông kề cạnh bên DE
=> BDEC là hình thang vuông.
a: Ta có: H đối xứng D qua AB
=>AH=AD và BH=BD
Xét ΔAHB và ΔADB có
AH=AD
BH=BD
AB chung
Do đó: ΔAHB=ΔADB
=>\(\widehat{HAB}=\widehat{DAB}\)
=>AB là phân giác của góc DAH
=>\(\widehat{DAH}=2\cdot\widehat{HAB}\)
Ta có: H đối xứng E qua AC
=>AE=AH và CH=CE
Xét ΔAEC và ΔAHC có
AH=AE
EC=HC
AC chung
Do đó: ΔAEC=ΔAHC
=>\(\widehat{EAC}=\widehat{HAC}\)
=>AC là phân giác của góc HAE
=>\(\widehat{HAE}=2\cdot\widehat{HAC}\)
Ta có: \(\widehat{HAD}+\widehat{HAE}=\widehat{DAE}\)
=>\(\widehat{DAE}=2\cdot\left(\widehat{HAB}+\widehat{HAC}\right)\)
=>\(\widehat{DAE}=2\cdot\widehat{BAC}=180^0\)
=>D,A,E thẳng hàng
Ta có: ΔAHB=ΔADB
=>\(\widehat{ADB}=\widehat{AHB}=90^0\)
=>BD\(\perp\)DE tại D
TA có: ΔAHC=ΔAEC
=>\(\widehat{AEC}=\widehat{AHC}=90^0\)
=>CE\(\perp\)ED tại D
Ta có: BD\(\perp\)DE
CE\(\perp\)ED
Do đó: BD//CE
c: Ta có: AH=AD
AE=AH
Do đó: AE=AD
=>A là trung điểm của ED
Xét ΔHED có
HA là đường trung tuyến
\(HA=\dfrac{ED}{2}\)
Do đó: ΔHED vuông tại H
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
mà HB=DB và HC=CE
nên \(DB\cdot CE=AH^2\)
=>\(DB\cdot CE=\left(\dfrac{1}{2}DE\right)^2=\dfrac{1}{4}DE^2\)