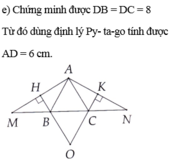
Cho tam giác ABC nhọn nội tiếp (O), AD là phân giác của góc BAC (D \(\in\) BC). Trên (O) lấyM và N sao cho BM // AD // CN. E,F,K lần lượt là giao của BN và AC, CM và AB, MN và AD. C/m:
1. Tam giác AMN cân
2. EF // MN
3. AE.NK = AF.MK
4.AD,ME,NF đồng quy
mik cần câu 4 mng ơiiiii!!