nhờ quý thầy cô giải giúp em voi ạ
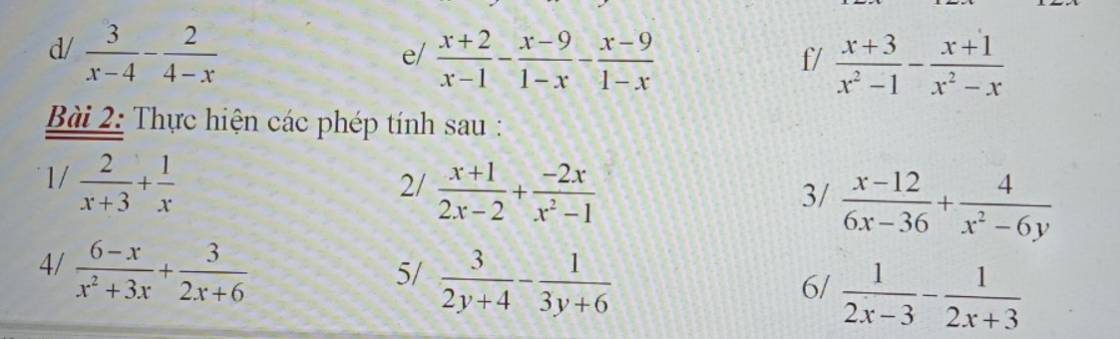
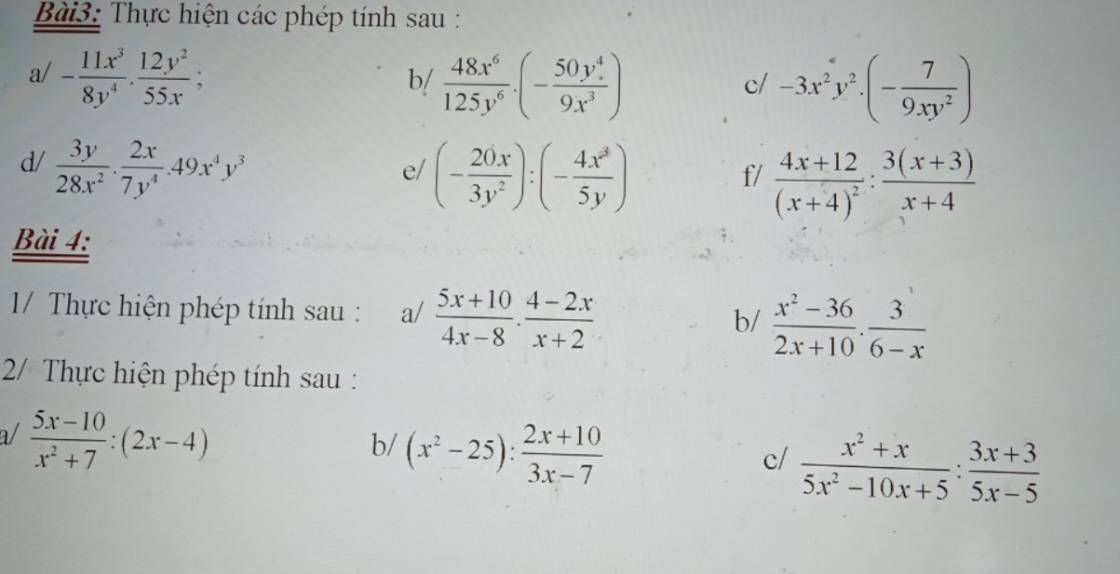

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



-Vì bài dài quá nên mình nói tóm tắt:
a) -Bạn chứng minh △ABM = △BCN (g-c-g) do có \(AB=BC\) , \(\widehat{BCN}=\widehat{ABM}=90^0\),\(\widehat{NBC}=\widehat{MAB}\) (bạn tự chứng minh).
-Suy ra: \(BM=CN\) .
-Suy ra 2 điều:
+\(QM^2-BQ^2=MN^2-MC^2\)
+\(QM+BQ=MN+MC\) (1)
\(QM^2-BQ^2=MN^2-MC^2\)
\(\Rightarrow\left(QM-BQ\right)\left(QM+BQ\right)=\left(MN-MC\right)\left(MN+MC\right)\)
\(\Rightarrow QM-BQ=MN-MC\) (2)
-Từ (1),(2) suy ra \(QM=MN\) nên △BMQ=△CNM (ch-cgv).
\(\Rightarrow\) MQ vuông góc với MN (bạn tự c/m).
\(QM=MN\) nên \(BQ=MC\) nên \(AQ=BM\Rightarrow PQ^2-AP^2=QM^2-BQ^2;QM+BQ=PQ+AP\)
Nên \(PQ=QM;\Delta APQ=\Delta BQM\) nên PQ⊥QM ; AP=BQ nên PQ=AQ
-Từ PQ=AQ bạn tự c/m PN=PQ (theo sườn mình đã cho) rồi sau đó c/m tam giác APQ=tam giác DNP rồi từ đó suy ra PQ vuông góc PN
.......

Hai câu c và d chỉ là BĐT \(\left(x+y+z\right)^2\ge3\left(xy+yz+zx\right)\), cách chứng minh \(\left(x+y+z\right)^2\ge3\left(xy+yz+zx\right)\) thế nào thì chứng minh c và d như vậy (biến đổi thành tổng của 3 bình phương các hiệu)
Với câu c thì \(x=ab;y=bc;z=ca\), câu d thì \(x=a^2b;y=...\)
Nhờ thầy viết cho em vài dòng câu d với ạ, câu d em chưa xử lý được thầy ạ?



CÁc số tròn chục nhỏ hơn 90 là :
10 ; 20 ; 30 ; 40 ; 50 ; 60 ; 70 ; 80
Tổng của các số tròn chục nhỏ hơn 90 là :
10 + 20 + ... + 80 = ( 80 + 10 ) x 8 : 2
= 90 x 8 : 2 = 720 : 2 = 360

Thực hiện lần lượt BĐT cô-si 3 số cho từng bộ 3 vế trái, ví dụ:
\(\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}\ge3\sqrt[3]{\dfrac{1}{a^3b^3c^3}}=\dfrac{3}{abc}\)
Làm tương tự, sau đó cộng vế và quy đồng vế phải là sẽ được BĐT cần chứng minh

Lời giải:
Hiệu số tuổi giữa 2 anh em không đổi, tức là 5 năm trước anh cũng hơn em 5 tuổi
Coi tuổi em 5 năm trước là 1 phần thì tuổi anh 5 năm trước là 2 phần.
Hiệu số phần bằng nhau: $2-1=1$ (phần)
Tuổi em 5 năm trước: $5:1\times 1=5$ (tuổi)
Tuổi em hiện nay: $5+5=10$ (tuổi)
Tuổi anh hiện nay: $10+5=15$ (tuổi)

Bài 7:
a. \(x+\dfrac{2}{5}=\dfrac{6}{7}\)
\(x=\dfrac{6}{7}-\dfrac{2}{5}=\dfrac{16}{35}\)
b. \(x=6,3.1,5=9,45\)
Câu 8:
Đáy bé là: \(\dfrac{2}{3}.120=80\) m
Diện tích thửa ruộng là:
( 120 + 80) x 76 : 2 = 7600 m vuông
Số kg thu hoạch được là:
7600 : 100 x 64,5 = 4902 kg
Đổi 4902 kg = 49,02 tạ thóc
Bài 12:
a: ĐKXĐ: \(x\notin\left\{3;2\right\}\)
b: Đặt \(A=\dfrac{x^2-4}{\left(x-3\right)\left(x-2\right)}\)
\(=\dfrac{\left(x-2\right)\left(x+2\right)}{\left(x-3\right)\left(x-2\right)}\)
\(=\dfrac{x+2}{x-3}\)
Thay x=13 vào A, ta được:
\(A=\dfrac{13+2}{13-3}=\dfrac{15}{10}=\dfrac{3}{2}\)
Bài 4:
1:
a: ĐKXĐ: \(x\notin\left\{2;-2\right\}\)
\(\dfrac{5x+10}{4x-8}\cdot\dfrac{4-2x}{x+2}\)
\(=\dfrac{5\left(x+2\right)}{4\left(x-2\right)}\cdot\dfrac{-2\left(x-2\right)}{x+2}\)
\(=\dfrac{-10}{4}=-\dfrac{5}{2}\)
b: ĐKXĐ: \(x\notin\left\{-5;6\right\}\)
\(\dfrac{x^2-36}{2x+10}\cdot\dfrac{3}{6-x}\)
\(=\dfrac{\left(x-6\right)\left(x+6\right)}{2\left(x+5\right)}\cdot\dfrac{-3}{x-6}\)
\(=\dfrac{-3\left(x+6\right)}{2\left(x+5\right)}\)
2:
a: ĐKXĐ: x<>2
\(\dfrac{5x-10}{x^2+7}:\left(2x-4\right)\)
\(=\dfrac{5\left(x-2\right)}{x^2+7}:2\left(x-2\right)\)
\(=\dfrac{5\left(x-2\right)}{2\left(x-2\right)\left(x^2+7\right)}=\dfrac{5}{2\left(x^2+7\right)}\)
b: ĐKXĐ: \(x\notin\left\{-5;\dfrac{7}{3}\right\}\)
\(\left(x^2-25\right):\dfrac{2x+10}{3x-7}\)
\(=\left(x^2-25\right)\cdot\dfrac{3x-7}{2x+10}\)
\(=\left(x-5\right)\left(x+5\right)\cdot\dfrac{3x-7}{2\left(x+5\right)}\)
\(=\dfrac{\left(x-5\right)\left(3x-7\right)}{2}\)
c: ĐKXĐ: \(x\notin\left\{1;-1\right\}\)
\(\dfrac{x^2+x}{5x^2-10x+5}:\dfrac{3x+3}{5x-5}\)
\(=\dfrac{x\left(x+1\right)}{5\left(x-1\right)^2}\cdot\dfrac{5\left(x-1\right)}{3\left(x+1\right)}\)
\(=\dfrac{x}{3\left(x-1\right)}\)