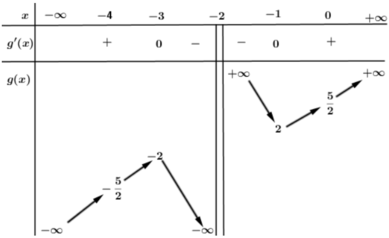
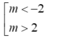Cho hàm số $y=x^3-3 m x^2+4 m^2-2$ có đồ thị $(C), m$ là tham số và điểm $C(1 ; 4)$. Tìm tất cả các giá trị của tham số $m$ để $(C)$ có hai điểm cực trị $A, B$ sao cho tam giác $A B C$ có diện tích bằng 4 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 2:
Thay x=0 và y=-3 vào (d), ta được:
m+2=-3
hay m=-5

Phương trình hoành độ giao điểm
x3+2mx2+3(m-1)x+2 =-x+2 hay x(x2+2mx+3(m-1))=0
suy ra x=0 hoặc x2+2mx+3(m-1)=0 (1)
Đường thẳng d cắt (C) tại ba điểm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân biệt khác 0
⇔ m 2 - 3 m + 3 > 0 m - 1 ≠ 0 ⇔ ∀ m m ≠ 1 ⇔ m ≠ 1
Khi đó ta có: C( x1 ; -x1+2) ; B(x2 ; -x2+2) trong đó x1 ; x2 là nghiệm của (1) ; nên theo Viet thì x 1 + x 2 = - 2 m x 1 x 2 = 3 m - 3
Vậy
C B → = ( x 2 - x 1 ; - x 2 + x 1 ) ⇒ C B = 2 ( x 2 - x 1 ) 2 = 8 ( m 2 - 3 m + 3 )
d ( M ; ( d ) ) = - 3 - 1 + 2 2 = 2
Diện tích tam giác MBC bằng khi và chỉ khi
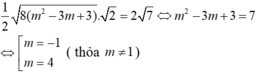
Chọn B.

x^2+(y-1)^2=4
=>R=2 và I(0;1)
A(1;1-m) thuộc (C)
y'=4x^3-4mx
=>y'(1)=4-4m
PT Δsẽ là y=(4-m)(x-1)+1-m
Δ luôn đi qua F(3/4;0) và điểm F nằm trong (λ)
Giả sử (Δ) cắt (λ) tại M,N
\(MN=2\sqrt{R^2-d^2\left(I;\Delta\right)}=2\sqrt{4-d^2\left(I;\Delta\right)}\)
MN min khi d(I;(Δ)) max
=>d(I;(Δ))=IF
=>Δ vuông góc IF
Khi đó, Δ có 1 vecto chỉ phương là: vecto u vuông góc với vecto IF=(3/4;p-1)
=>vecto u=(1;4-4m)
=>1*3/4-(4-4m)=0
=>m=13/16

Lời giải:
1.PT hoành độ giao điểm:
$x^2-mx-4=0(*)$
Khi $m=3$ thì pt trở thành: $x^2-3x-4=0$
$\Leftrightarrow (x+1)(x-4)=0$
$\Rightarrow x=-1$ hoặc $x=4$
Với $x=-1$ thì $y=(-1)^2=1$. Giao điểm thứ nhất là $(-1;1)$
Với $x=4$ thì $y=4^2=16$. Giao điểm thứ hai là $(4;16)$
2.
$\Delta (*)=m^2+16>0$ với mọi $m\in\mathbb{R}$ nên PT $(*)$ luôn có 2 nghiệm phân biệt $x_1,x_2$, đồng nghĩa với việc 2 ĐTHS luôn cắt nhau tại 2 điểm phân biệt $A(x_1,y_1); B(x_2,y_2)$
Áp dụng định lý Viet:
$x_1+x_2=m$ và $x_1x_2=-4$
Khi đó:
$y_1^2+y_2^2=49$
$\Leftrightarrow (mx_1+4)^2+(mx_2+4)^2=49$
$\Leftrightarrow m^2(x_1^2+x_2^2)+8m(x_1+x_2)=17$
$\Leftrightarrow m^2[(x_1+x_2)^2-2x_1x_2]+8m(x_1+x_2)=17$
$\Leftrightarrow m^2(m^2+8)+8m^2=17$
$\Leftrightarrow m^4+16m^2-17=0$
$\Leftrightarrow (m^2-1)(m^2+17)=0$
$\Rightarrow m^2=1$
$\Leftrightarrow m=\pm 1$

a) Xét hàm số \(y=ax^4+bx^2+c\)
Ta có \(y'=4ax^3+2bx=2x\left(2ax^2+b\right)\)
\(y'=0\Leftrightarrow x=0\) hoặc \(2ax^2+b=0\left(1\right)\)
Đồ thị hàm số có 3 cực trị phân biệt khi và chỉ khi \(y'=0\) có 3 nghiệm phân biệt hay phương trình (1) có 2 nghiệm phân biệt khác 0 \(\Leftrightarrow ab< 0\) (*)
Với điều kiện (*) thì đồ thị có 3 điểm cực trị là :
\(A\left(0;c\right);B\left(-\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right);C\left(\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right)\)
Ta có \(AB=AC=\sqrt{\frac{b^2-8ab}{16a^2}};BC=\sqrt{-\frac{2b}{a}}\) nên tam giác ABC vuông khi và chỉ khi vuông tại A.
Khi đó \(BC^2=2AB^2\Leftrightarrow b^3+8a=0\)
Do đó yêu cầu bài toán\(\Leftrightarrow\begin{cases}ab< 0\\b^3+8a=0\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\-8\left(m+1\right)^3+8=0\end{cases}\)\(\Leftrightarrow m=0\)
b) Ta có yêu cầu bài toán \(\Leftrightarrow\begin{cases}ab< 0\\OA=BC\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\m^2-4\left(m+1\right)=0\end{cases}\)
\(\Leftrightarrow m=2\pm2\sqrt{2}\)

1.
Đồ thị hàm bậc 3 có 2 điểm cực trị nằm về 2 phía trục hoành khi và chỉ khi \(f\left(x\right)=0\) có 3 nghiệm phân biệt
\(\Leftrightarrow x^3+3x^2+mx+m-2=0\) có 3 nghiệm pb
\(\Leftrightarrow x^3+3x^2-2+m\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2x-2\right)+m\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2x+m-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^2+2x+m-2=0\left(1\right)\end{matrix}\right.\)
Bài toán thỏa mãn khi (1) có 2 nghiệm pb khác -1
\(\Leftrightarrow\left\{{}\begin{matrix}1-2+m-2\ne0\\\Delta'=1-\left(m-2\right)>0\end{matrix}\right.\)
\(\Leftrightarrow m< 3\)
2.
Pt hoành độ giao điểm:
\(\dfrac{2x-2}{x+1}=2x+m\)
\(\Rightarrow2x-2=\left(2x+m\right)\left(x+1\right)\)
\(\Leftrightarrow2x^2+mx+m+2=0\) (1)
d cắt (C) tại 2 điểm pb \(\Rightarrow\) (1) có 2 nghiệm pb
\(\Rightarrow\Delta=m^2-8\left(m+2\right)>0\Rightarrow\left[{}\begin{matrix}m>4+4\sqrt{2}\\m< 4-4\sqrt{2}\end{matrix}\right.\)
Khi đó, theo hệ thức Viet: \(\left\{{}\begin{matrix}x_A+x_B=-\dfrac{m}{2}\\x_Ax_B=\dfrac{m+2}{2}\end{matrix}\right.\)
\(y_A=2x_A+m\) ; \(y_B=2x_B+m\)
\(\Rightarrow AB^2=\left(x_A-x_B\right)^2+\left(y_A-y_B\right)^2=5\)
\(\Leftrightarrow\left(x_A-x_B\right)^2+\left(2x_A-2x_B\right)^2=5\)
\(\Leftrightarrow\left(x_A-x_B\right)^2=1\)
\(\Leftrightarrow\left(x_A+x_B\right)^2-4x_Ax_B=1\)
\(\Leftrightarrow\left(-\dfrac{m}{2}\right)^2-4\left(\dfrac{m+2}{2}\right)=1\)
\(\Leftrightarrow m^2-8m-20=0\Rightarrow\left[{}\begin{matrix}m=10\\m=-2\end{matrix}\right.\)

Đường tròn (S) tâm \(I\left(-1;-3\right)\) bán kính \(R=3\)
Thế tọa độ A vào pt (S) thỏa mãn nên A nằm trên đường tròn
Ta cần tìm B, C sao cho chi vi ABC lớn nhất
Đặt \(\left(AB;AC;BC\right)=\left(c;b;a\right)\Rightarrow\dfrac{a}{sinA}=\dfrac{b}{sinB}=\dfrac{c}{sinC}=2R\)
\(\Rightarrow a+b+c=2R\left(sinA+sinB+sinC\right)\)
Mặt khác ta có BĐT quen thuộc \(sinA+sinB+sinC\le\dfrac{3\sqrt{3}}{2}\)
Dấu "=" xảy ra khi tam giác ABC đều
\(\Rightarrow a=b=c=2R.sin60^0=3\sqrt{3}\)
Khi đó I đồng thời là trọng tâm kiêm trực tâm \(\Rightarrow\left\{{}\begin{matrix}BC\perp AI\\d\left(A;BC\right)=\dfrac{a\sqrt{3}}{2}=\dfrac{9}{2}\end{matrix}\right.\)
\(\Rightarrow\) Phương trình BC có dạng \(y=-\dfrac{3}{2}\)
Hay (Cm) có 1 tiếp tuyến là \(y=-\dfrac{3}{2}\) (hệ số góc bằng 0 nên tiếp tuyến này đi qua 2 cực tiểu)
\(\Rightarrow m=-1\)

Xét phương trình f’ (x) = x2+(4-m) x+5-2m=0
⇔ x 2 + 4 x + 5 = m ( x + 2 ) ⇔ g ( x ) = x 2 + 4 x + 5 x + 2 = m
Ta có nghiệm của f’ (x)=0 cũng là hoành độ giao điểm của g(x)=m
Khi đó từ bảng biến thiên ta có YCBT khi m> 2.
Chọn A.