hệ số lớn nhất trong khai triển của (2x+1)^4 là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 6 2018
mk bổ sung thêm hằng đẳng thức cho các bạn nha .
ta có : \(\left(a+b\right)^{10}=a^{10}+10a^9b+45a^8b^2+120a^7b^3+210a^6b^4+252a^5b^5+210a^4b^6+120a^3b^7+45a^2b^8+10ab^9+b^{10}\)
\(\Rightarrow\left(1+\dfrac{2x}{3}\right)^{10}=1+\dfrac{20x}{3}+20x^2+\dfrac{320x^3}{9}+\dfrac{1120x^4}{27}+\dfrac{896x^5}{27}+\dfrac{4480x^6}{243}+\dfrac{5120x^7}{729}+\dfrac{1280x^8}{729}+\dfrac{5120x^9}{19683}+\dfrac{340x^{10}}{19683}\)
ta thấy hệ số lớn nhất trong khai triển này là \(\dfrac{1120}{27}\)
vậy hệ số lớn nhất trong khai triển \(\left(1+\dfrac{2x}{3}\right)^{10}\) là \(\dfrac{1120}{27}\) .
nhớ hok thuộc hằng đẳng thức mới này nha 
.
3 tháng 8 2018
ta có : \(\left(1+\dfrac{2x}{3}\right)^{10}=\sum\limits^{10}_{k=0}\left(\dfrac{2}{3}\right)^k.x^k\)
vì \(0< \dfrac{2}{3}< 1\) \(\Rightarrow\left(\dfrac{2}{3}\right)^{k-1}>\left(\dfrac{2}{3}\right)^k\)
mà vì \(K\in N\)
\(\Rightarrow\) hệ số lớn nhất trong khai triển \(\left(1+\dfrac{2x}{3}\right)^{10}\) là \(\left(\dfrac{2}{3}\right)^0=1\)
AH
Akai Haruma
Giáo viên
13 tháng 12 2017
Lời giải:
Theo khai triển nhị thức Newton ta có:
\(\left ( 1+\frac{2x}{3} \right )^{10}=\sum _{k=0}^{10}C^{k}_{10} 1^{k}\left ( \frac{2x}{3} \right )^{10-k}\)
\(=C^{0}_{10}\left ( \frac{2x}{3} \right )^{10}+C_{10}^{1}\left ( \frac{2x}{3} \right )^9+.....+C_{10}^{10}\left ( \frac{2x}{3} \right )^0\)
Các hệ số: \(C_{10}^0(\frac{2}{3})^{10}; C_{10}^{1}(\frac{2}{3})^9; ...; C_{10}^{10}(\frac{2}{3})^0\)
Xét hàm: \(f(x)=C_{10}^{x}\left(\frac{2}{3}\right)^{10-x}\)
\(f(a+1)=C_{10}^{a+1}(\frac{2}{3})^{9-a}\)
\(f(a)=C_{10}^{a}\left(\frac{2}{3}\right)^{10-a}\)
\(f(a+1)-f(a)=\frac{10!}{(a+1)!(9-a)!}\frac{2^{9-a}}{3^{9-a}}-\frac{10!}{a!(10-a)!}\frac{2^{10-a}}{3^{10-a}}\)
\(=\frac{10!.2^{9-a}}{a!(9-a)!.3^{9-a}}\left[ \frac{1}{a+1}-\frac{2}{3(10-a)}\right]\)
\(=\frac{10!.2^{9-a}}{a!(9-a)!.3^{9-a}}.\frac{28-5a}{3(a+1)(10-a)}\)
Nếu \(a\geq 6\Rightarrow f(a+1)-f(a)< 0\Rightarrow \) hàm giảm
Nếu \(a\leq 6\Rightarrow f(a+1)-f(a)> 0\) , hàm tăng
Do đó điểm cực đại của \(f(x)\) với \(x=0;1;2;....; 10\) đặt tại \(x=6\)
Do đó hệ số lớn nhất là: \(C_{10}^{6}(\frac{2}{3})^4=\frac{1120}{27}\)
30 tháng 12 2018
bạn ơi cho mình hỏi !
tại sao giá trị k ở C lại là 6 mà (2/3)4
HQ
Hà Quang Minh
Giáo viên
1 tháng 10 2023
Ta có:
\({(2x + 3)^5} = 32{x^5} + 240{x^4} + 720{x^3} + 1080{x^2} + 810x + 243\)
Hệ số của \({x^3}\) là 720
Hệ số của \({x^4}\) là 240.
Vậy hệ số của \({x^3}\) lớn hơn hệ số của \({x^4}\).
CM
9 tháng 12 2018
Đáp án A.
Ta có A n 5 ≤ 18 A n - 2 4 ⇔ n ≥ 6 n ! n - 5 ! ≤ 18 . n - 2 ! n - 6 ! ⇔ n ≥ 6 n n - 1 n - 5 ≤ 18 ⇔ 9 ≤ n ≤ 10 → n = 10 .
Với n = 10, xứt khai triển nhị thức
2 x + 1 x x 10 = ∑ k = 10 10 C 10 k . 2 x 10 - k . 1 x 5 x = ∑ k = 0 10 C 10 k . 2 10 - k . x 10 - 6 k 5 .
Hệ số của x 4 ứng với 10 - 6 k 5 = 4 ⇔ k = 5 . Vậy hệ số cần tìm là C 10 5 . 2 5 = 8064 .
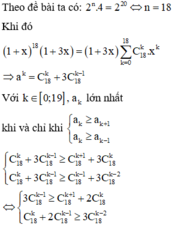
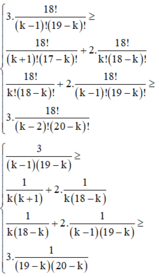
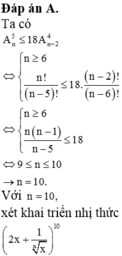
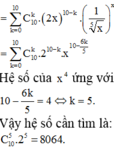
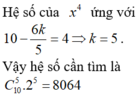
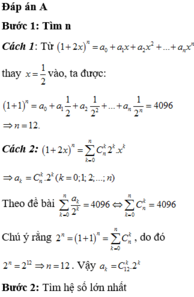
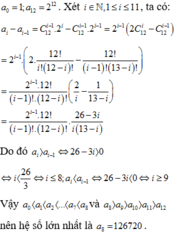
\(\left(2x+1\right)^4=C^0_4\cdot\left(2x\right)^4\cdot1^0+C^1_4\cdot\left(2x\right)^3\cdot1^1+C^2_4\cdot\left(2x\right)^2\cdot1^2+C^3_4\cdot\left(2x\right)^1\cdot1^3+C^4_4\cdot\left(2x\right)^0\cdot1^4\)
\(=16x^4+32x^3+24x^2+8x+1\)
Hệ số lớn nhất là 32