Question

[TỐNG HOÀNG SANG]

 

Answer 1

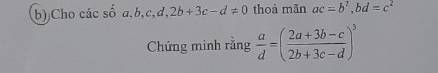
[Akai Haruma]

Lời giải:

$ac=b^2\Rightarrow \frac{a}{b}=\frac{b}{c}$

$bd=c^2\Rightarrow \frac{b}{c}=\frac{c}{d}$

$\Rightarrow \frac{a}{b}=\frac{b}{c}=\frac{c}{d}$

Đặt $\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=k\Rightarrow a=bk; b=ck; c=dk$
Khi đó:

$\frac{a}{d}=\frac{bk}{d}=\frac{ck^2}{d}=\frac{dk^3}{d}=k^3(1)$

Lại có:

$(\frac{2a+3b-c}{2b+3c-d})^3=(\frac{2bk+3b-c}{2ck+3c-d})^3=(\frac{2ck^2+3ck-c}{2dk^2+3dk-d})^3$
$=[\frac{c(2k^2+3k-1)}{d(2k^2+3k-1)}]^3=(\frac{c}{d})^3=(\frac{dk}{d})^3=k^3(2)$
Từ $(1); (2)$ ta có đpcm.