cho tam giác ABC vuông tại A có AB < AC, đường cao AH.
a) chứng minh AB . AC = AH . BC
b) Gọi D và E lần lượt là trung điểm của AB, BC. Chứng minh CH . CB = 4DE^2
c) Gọi M là giao điểm của đường thẳng vuông góc với BC tại B và DE.Gọi N là giao điểm của AH và CM. Chứng minh N là trung điểm của...
Đọc tiếp
cho tam giác ABC vuông tại A có AB < AC, đường cao AH.
a) chứng minh AB . AC = AH . BC
b) Gọi D và E lần lượt là trung điểm của AB, BC. Chứng minh CH . CB = 4DE^2
c) Gọi M là giao điểm của đường thẳng vuông góc với BC tại B và DE.Gọi N là giao điểm của AH và CM. Chứng minh N là trung điểm của AH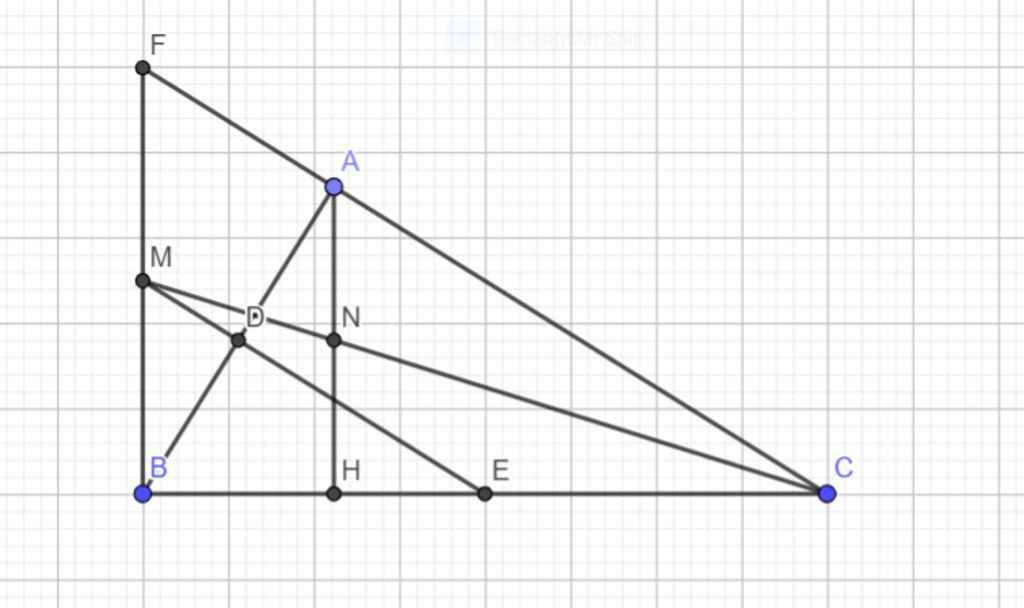 
a: ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\left(1\right)\)
ΔABC có AH là đường cao
nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC\left(2\right)\)
Từ (1) và (2) suy ra \(AB\cdot AC=AH\cdot BC\)
b: Xét ΔABC có
D,E lần lượt là trung điểm của BA,BC
=>DE là đường trung bình của ΔABC
=>DE//AC và DE=1/2AC
=>AC=2DE
Xét ΔCHA vuông tại H và ΔCAB vuông tại A có
\(\widehat{HCA}\) chung
Do đó: ΔCHA~ΔCAB
=>\(\dfrac{CH}{CA}=\dfrac{CA}{CB}\)
=>\(CH\cdot CB=CA^2=4DE^2\)