giúp mik bài 2 vs ạ mik cần gấp 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 1 2022
Bài 2:
a: Xét ΔABC có
X là trung điểm của BC
Y là trung điểm của AB
Do đó: XY là đường trung bình
=>XY//AC và XY=AC/2=3,5(cm)
hay XZ//AC và XZ=AC
b: Xét tứ giác AZBX có
Y là trung điểm của AB
Y là trung điểm của ZX
Do đó: AZBX là hình bình hành
mà \(\widehat{AXB}=90^0\)
nên AZBX là hình chữ nhật
d: Xét tứ giác AZXC có
XZ//AC
XZ=AC
Do đó: AZXC là hình bình hành
TK
1
17 tháng 10 2021
Câu 3:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3}=\dfrac{y}{2}=\dfrac{x+y}{3+2}=\dfrac{90}{5}=18\)
Do đó: x=54; y=36
NT
6 tháng 9 2021
c. \(\left|\dfrac{8}{4}-\left|x-\dfrac{1}{4}\right|\right|-\dfrac{1}{2}=\dfrac{3}{4}\)
\(\Rightarrow\left[{}\begin{matrix}\left|\dfrac{8}{4}-x+\dfrac{1}{4}\right|-\dfrac{1}{2}=\dfrac{3}{4}\\\left|\dfrac{8}{4}+x-\dfrac{1}{4}\right|-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\left|\dfrac{9}{4}-x\right|-\dfrac{1}{2}=\dfrac{3}{4}\\\left|\dfrac{7}{4}+x\right|-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}\dfrac{9}{4}-x-\dfrac{1}{2}=\dfrac{3}{4}\\x=\dfrac{9}{4}-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\\\left[{}\begin{matrix}\dfrac{7}{4}+x-\dfrac{1}{2}=\dfrac{3}{4}\\-\dfrac{7}{4}-x-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}x=1\\x=\dfrac{7}{2}\end{matrix}\right.\\\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=-3\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{7}{2}\\x=-3\end{matrix}\right.\)
Ở nơi x=9/4-1/2 là x-9/4-1/2 nha
KK
6 tháng 9 2021
a. -1,5 + 2x = 2,5
<=> 2x = 2,5 + 1,5
<=> 2x = 4
<=> x = 2
b. \(\dfrac{3}{2}\left(x+5\right)-\dfrac{1}{2}=\dfrac{4}{3}\)
<=> \(\dfrac{3}{2}x+\dfrac{15}{2}-\dfrac{1}{2}=\dfrac{4}{3}\)
<=> \(\dfrac{9x}{6}+\dfrac{45}{6}-\dfrac{3}{6}=\dfrac{8}{6}\)
<=> 9x + 45 - 3 = 8
<=> 9x = 8 + 3 - 45
<=> 9x = -34
<=> x = \(\dfrac{-34}{9}\)
3 tháng 9 2021
b: Xét ΔABE vuông tại A có AH là đường cao ứng với cạnh huyền BE
nên \(BH\cdot BE=AB^2\left(1\right)\)
Xét ΔABC vuông tại B có BH là đường cao ứng với cạnh huyền AC
nên \(AH\cdot AC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BE=AH\cdot AC\)
PL
2
30 tháng 8 2021
Câu 3:
a: Ta có: \(2x\left(3x-1\right)-\left(x-3\right)\left(6x+2\right)\)
\(=6x^2-2x-6x^2-2x+18x+6\)
=14x+6
b: Ta có: \(2x\left(x+7\right)-3x\left(x+1\right)\)
\(=2x^2+14x-3x^2-3x\)
\(=-x^2+11x\)
30 tháng 8 2021
Câu 2:
a: Ta có: \(\left(-8x^5+12x^3-16x^2\right):4x^2\)
\(=-8x^5:4x^2+12x^3:4x^2-16x^2:4x^2\)
\(=-2x^3+3x-4\)
b: Ta có: \(\left(12x^3y^3-18x^2y+9xy^2\right):6xy\)
\(=12x^3y^3:6xy-18x^2y:6xy+9xy^2:6xy\)
\(=2x^2y^2-3x+\dfrac{3}{2}y\)
c: Ta có: \(\dfrac{x^3-11x^2+27x-9}{x-3}\)
\(=\dfrac{x^3-3x^2-8x^2+24x+3x-9}{x-3}\)
\(=x^2-8x+3\)
d: Ta có: \(\dfrac{6x^4-13x^3+7x^2-x-5}{3x+1}\)
\(=\dfrac{6x^4+2x^3-15x^3-5x^2+12x^2+4x-5x-\dfrac{5}{3}-\dfrac{10}{3}}{3x+1}\)
\(=2x^3-5x^2+4x-\dfrac{5}{3}-\dfrac{\dfrac{10}{3}}{3x+1}\)
27 tháng 9 2021
\(3,\\ a,\dfrac{2011}{2010}=1+\dfrac{1}{2010};\dfrac{3011}{3010}=1+\dfrac{1}{3010}\\ \dfrac{1}{2010}>\dfrac{1}{3010}\left(2010< 3010\right)\Rightarrow\dfrac{2011}{2010}>\dfrac{3011}{3010}\\ b,A=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\\ A=\left(1+\dfrac{1}{3}+...+\dfrac{1}{99}\right)-\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{100}\right)\\ A=\left(1+\dfrac{1}{3}+...+\dfrac{1}{99}\right)+\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{100}\right)-2\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{100}\right)\\ A=\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{100}\right)-\left(1+\dfrac{1}{2}+...+\dfrac{1}{50}\right)\\ A=\dfrac{1}{51}+\dfrac{1}{52}+....+\dfrac{1}{100}=B\)
\(4,\\ a,\dfrac{x+5}{x+1}=1+\dfrac{4}{x+1}\in Z\Leftrightarrow4⋮x+1\\ \Leftrightarrow x+1\inƯ\left(4\right)=\left\{-4;-2;-1;1;2;4\right\}\\ \Leftrightarrow x\in\left\{-5;-3;-2;0;1;3\right\}\\ b,\dfrac{2x+4}{x+3}=\dfrac{2\left(x+3\right)-2}{x+3}=2-\dfrac{2}{x+3}\in Z\\ \Leftrightarrow2⋮x+3\Leftrightarrow x+3\inƯ\left(2\right)=\left\{-2;-1;1;2\right\}\\ \Leftrightarrow x\in\left\{-5;-4;-2;-1\right\}\)
\(5,\\ -\left|3x+\dfrac{1}{5}\right|\le0\\ \Leftrightarrow A=2017-\left|3x+\dfrac{1}{5}\right|\le2017\\ A_{max}=2017\Leftrightarrow3x+\dfrac{1}{5}=0\Leftrightarrow x=-\dfrac{1}{15}\\ 6,\\ \left\{{}\begin{matrix}\left(x+\dfrac{1}{2}\right)^2\ge0\\\left|2y-\dfrac{3}{4}\right|\ge0\end{matrix}\right.\Leftrightarrow A=\left(x+\dfrac{1}{2}\right)^2+\left|2y-\dfrac{3}{4}\right|+\dfrac{175}{3}\ge\dfrac{175}{3}\\ A_{min}=\dfrac{175}{3}\Leftrightarrow\left\{{}\begin{matrix}x+\dfrac{1}{2}=0\\2y-\dfrac{3}{4}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=\dfrac{3}{8}\end{matrix}\right.\)
28 tháng 9 2021
Bài 5:
\(A=-\left|3x+\dfrac{1}{5}\right|+2017\le2017\forall x\)
Dấu '=' xảy ra khi \(x=-\dfrac{1}{15}\)
BA
1
21 tháng 7 2023
4*cos(pi/6-a)*sin(pi/3-a)
=4*(cospi/6*cosa+sinpi/6*sina)*(sinpi/3*cosa-sina*cospi/3)
=4*(căn 3/2*cosa+1/2*sina)*(căn 3/2*cosa-1/2*sina)
=4*(3/4*cos^2a-1/4*sin^2a)
=3cos^2a-sin^2a
=3(1-sin^2a)-sin^2a
=3-4sin^2a
=>m=3; n=-4
m^2-n^2=-7
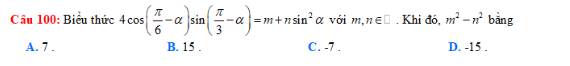
bài 2:
a: ĐKXĐ: \(x\notin\left\{1;-1\right\}\)
\(A=\dfrac{x^2-2x+1}{x-1}+\dfrac{x^2+2x+1}{x+1}-\dfrac{3}{1}\)
\(=\dfrac{\left(x-1\right)^2}{x-1}+\dfrac{\left(x+1\right)^2}{x+1}-3\)
=x-1+x+1-3
=2x-3
b: Thay x=3 vào A, ta được:
\(A=2\cdot3-3=3\)
Thay x=-1/2 vào A, ta được:
\(A=2\cdot\dfrac{-1}{2}-3=-1-3=-4\)